Types Of Polar Graphs Eowynconnell
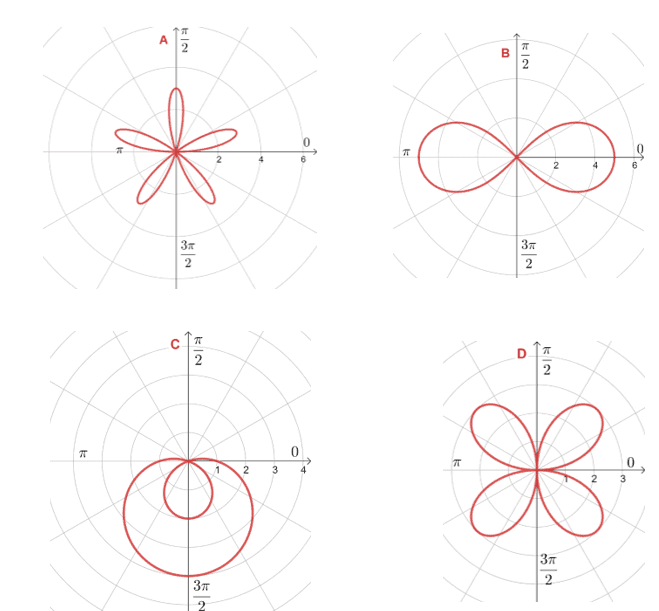
Types Of Polar Graphs Eowynconnell 1. r = 3 sin 5 θ, r = 3 sin 2 θ r = 1 – 3 sin θ, r 2 = 25 sin 2 θ. the polar curves of these four polar equations are as shown below. match the polar equations with their corresponding polar curve. 2. test whether r 2 = 16 sin 2 θ is symmetric with respect to the polar axis, the line θ = θ 2, or the pole. 3. 2 standard graphs in polar coordinates include circles and roses, cardioids and limaçons, lemniscates, and spirals. 3 to find the intersection points of the polar graphs r = f(θ) and r = g(θ) we solve the equation f(θ) = g(θ). in addition, we should always check whether the pole is a point on both graphs.
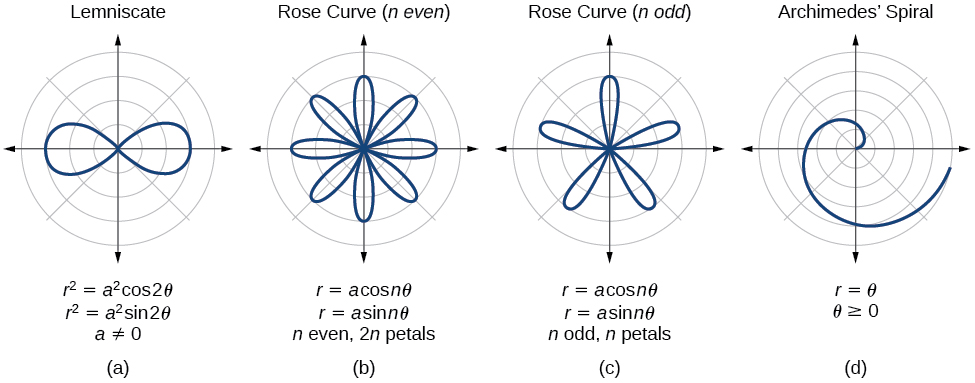
Types Of Polar Graphs Eowynconnell The graph of a polar equation can be evaluated for three types of symmetry, as shown in figure 2. figure 2 (a) a graph is symmetric with respect to the line θ = π 2 θ = π 2 ( y axis) if replacing ( r , θ ) ( r , θ ) with ( − r , − θ ) ( − r , − θ ) yields an equivalent equation. The process of sketching the graphs of these relations is very similar to that used to sketch graphs of functions in cartesian coordinates. consider a relation between polar coordinates of the form, \(r=f\left( \theta \right)\). to graph such a relation, first make a table of the form. Polar curves are defined by points that are a variable distance from the origin (the pole) depending on the angle measured off the positive x x axis. polar curves can describe familiar cartesian shapes such as ellipses as well as some unfamiliar shapes such as cardioids and lemniscates. r=1 \cos {\theta}\sin {3\theta} r = 1−cosθsin3θ. Example 9.2.7. find all intersection points of the graphs of r = 2 2sin(θ) and r = 2 2cos(θ). however, you can see in the figure that the graphs also appear to intersect at the pole. to verify that the pole indeed lies on both graphs, we can solve for in each equation when both points, , represent the pole.
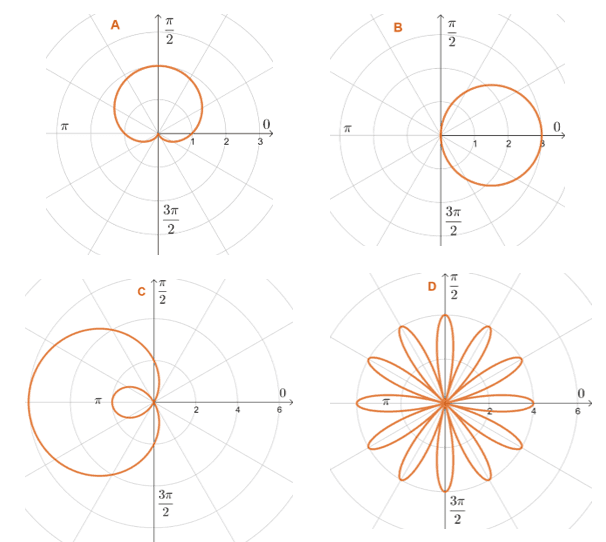
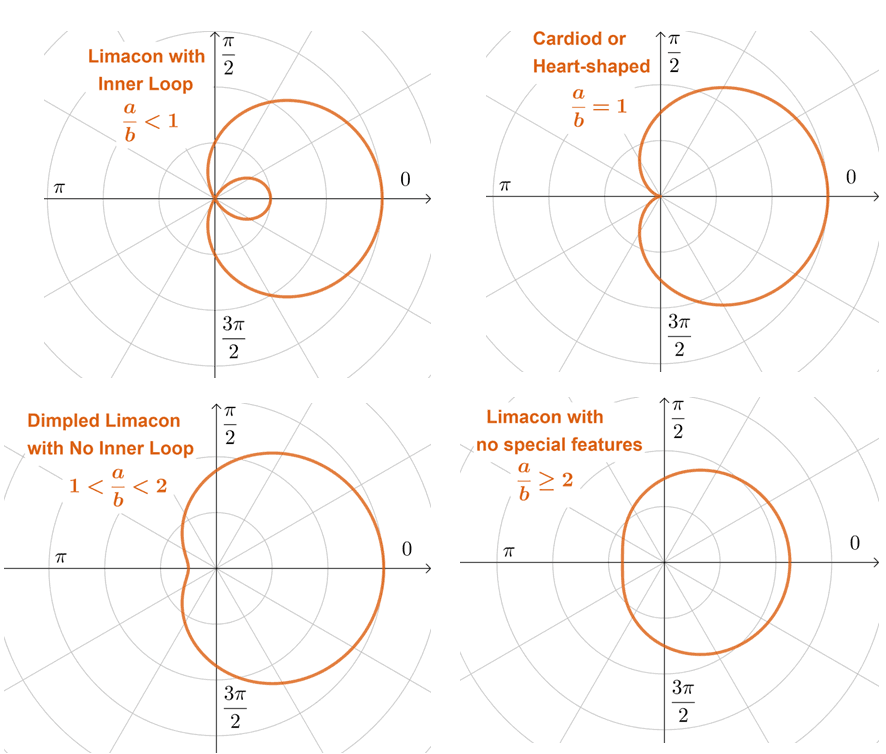
Types Of Polar Graphs Eowynconnell Polar curves are defined by points that are a variable distance from the origin (the pole) depending on the angle measured off the positive x x axis. polar curves can describe familiar cartesian shapes such as ellipses as well as some unfamiliar shapes such as cardioids and lemniscates. r=1 \cos {\theta}\sin {3\theta} r = 1−cosθsin3θ. Example 9.2.7. find all intersection points of the graphs of r = 2 2sin(θ) and r = 2 2cos(θ). however, you can see in the figure that the graphs also appear to intersect at the pole. to verify that the pole indeed lies on both graphs, we can solve for in each equation when both points, , represent the pole. Example 1: graph the polar equation r = 1 – 2 cos θ. solution: identify the type of polar equation . the polar equation is in the form of a limaçon, r = a – b cos θ. find the ratio of . a b. to determine the equation’s general shape . a b = 1 2 since the ratio is less than 1, it will have both an inner and outer loop. the loops will. 1. describe the three types of symmetry in polar graphs, and compare them to the symmetry of the cartesian plane. 2. which of the three types of symmetries for polar graphs correspond to the symmetries with respect to the x axis, y axis, and origin? 3. what are the steps to follow when graphing polar equations? 4.

Types Of Polar Graphs Eowynconnell Example 1: graph the polar equation r = 1 – 2 cos θ. solution: identify the type of polar equation . the polar equation is in the form of a limaçon, r = a – b cos θ. find the ratio of . a b. to determine the equation’s general shape . a b = 1 2 since the ratio is less than 1, it will have both an inner and outer loop. the loops will. 1. describe the three types of symmetry in polar graphs, and compare them to the symmetry of the cartesian plane. 2. which of the three types of symmetries for polar graphs correspond to the symmetries with respect to the x axis, y axis, and origin? 3. what are the steps to follow when graphing polar equations? 4.
Types Of Polar Graphs Eowynconnell

Comments are closed.