Suma De Matrices Propiedades De La Suma De Matrices Diferencia De Matrices Ejemplos Y Graficos

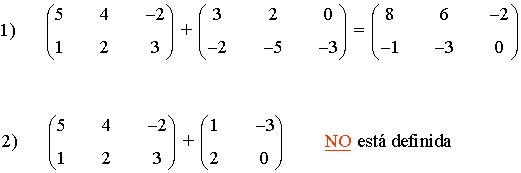
Suma De Matrices Propiedades De La Suma De Matrices Diferencia De Matrices Ejemplos Y Gráficos Propiedad cerradura. para sumar matrices se debe tener en cuenta que tengan las mismas dimensiones, es decir si quiero sumar dos matrices, ambas deben tener dimensiones m x n. veamos un ejemplo. por ejemplo, si quiero sumar una matriz 3 x 2, entonces deberá ser con otra matriz que también tenga dimensiones 3 x 2. Resta de matrices: conceptos y ejemplos. la resta de matrices funciona de manera similar a la suma de matrices. en lugar de sumar los elementos correspondientes, simplemente se restan. para realizar una resta de matrices, ambas matrices deben ser del mismo tamaño. por ejemplo, si tenemos:.

Propiedades De La Suma De Matrices Flexi dice: las propiedades de la suma de matrices son las siguientes: propiedad de clausura: la suma de dos matrices siempre es una matriz del mismo tamaño que las matrices originales. propiedad conmutativa: el orden de la suma no importa. para cualesquiera dos matrices \mathbf {a} y \mathbf {b} del mismo tamaño, a b = b a. Ejemplos y gráficos. suma de matrices. la suma de dos matrices a = ( a ij ) y b = ( b ij ) de la misma dimensión m × n, es otra matriz que representamos como a b, de la misma dimensión que a y b, cuyos elementos son la suma de los elementos situados en las mismas posiciones, es decir, a b = (a ij b ij). La operación se define de una manera muy sencilla: la matriz suma de dos matrices con la misma dimensión es la matriz que tiene en la posición fila i y columna j la suma de los elementos de la misma posición en las matrices que sumamos. es decir, la suma de matrices se calcula sumando los elementos que ocupan la misma posición. Suma y diferencia de matrices. la suma de dos matrices a= (a ij), b= (b ij) de la misma dimensión, es otra matriz s= (s ij) de la misma dimensión que los sumandos y con término genérico s ij =a ij b ij. por tanto, para poder sumar dos matrices estas han de tener la misma dimensión. la suma de las matrices a y b se denota por a b.