Solution Desvelando Las Propiedades De Los Determinantes Una Introduccion Al Algebra Lineal

Solution Desvelando Las Propiedades De Los Determinantes Una Introducción Al álgebra Lineal Propiedad 1: determinante de la matriz transpuesta. 2. propiedad 2: determinante con una fila o columna llena de ceros. 3. propiedad 3: determinante con dos filas o columnas iguales. 4. propiedad 4: cambiar filas o columnas de un determinante. 5. propiedad 5: multiplicar una línea de una determinante por un escalar. Usando la definición 3.1.1 podemos encontrar el determinante de la siguiente manera: det (a) = 3 × 4 − 2 × 6 = 12 − 12 = 0 por teorema no3.2.7a es invertible. ahora considere la matriz b. nuevamente por definición 3.1.1 tenemos det (b) = 2 × 1 − 5 × 3 = 2 − 15 = − 13 por teorema 3.2.7b es invertible y el determinante de la.

Solution Desvelando Las Propiedades De Los Determinantes Una Introducción Al álgebra Lineal Los determinantes tienen varias propiedades importantes que los hacen útiles en álgebra lineal y cálculo. a continuación se describen algunas de las propiedades más comunes: propiedad 1: el determinante de una matriz se mantiene igual si se intercambian filas o columnas. propiedad 2: el determinante de una matriz se multiplica por un. Our resource for Álgebra lineal: una introducción moderna includes answers to chapter exercises, as well as detailed information to walk you through the process step by step. with expert solutions for thousands of practice problems, you can take the guesswork out of studying and move forward with confidence. Propiedades básicas de los determinantes. las propiedades de los determinantes son cruciales para realizar cálculos eficientes y comprender el comportamiento de las matrices. a continuación, se enumeran algunas de las más importantes: determinante de la matriz identidad: el determinante de la matriz identidad es 1, es decir, det (i) = 1. Ejercicios resueltos paso a paso. en esta lección vamos a ver las propiedades de los determinantes. las propiedades de los determinantes nos permiten calcular un determinante sin necesidad de desarrollarlo, lo cual es especialmente útil en determinantes cuyos elementos sean letras o que su desarrollo sea algo complejo.

Solution Desvelando Las Propiedades De Los Determinantes Una Introducción Al álgebra Lineal Propiedades básicas de los determinantes. las propiedades de los determinantes son cruciales para realizar cálculos eficientes y comprender el comportamiento de las matrices. a continuación, se enumeran algunas de las más importantes: determinante de la matriz identidad: el determinante de la matriz identidad es 1, es decir, det (i) = 1. Ejercicios resueltos paso a paso. en esta lección vamos a ver las propiedades de los determinantes. las propiedades de los determinantes nos permiten calcular un determinante sin necesidad de desarrollarlo, lo cual es especialmente útil en determinantes cuyos elementos sean letras o que su desarrollo sea algo complejo. Es como álgebra y probabilidad. .1.1. introducción a los determinanteslos determinantes están definidos pa. a matrices cuadradas, es decir, de nxn. el determinante de una. atriz cuadrada es un escalar (número). nos apoyaremos en las matrices de 2x2 para describir cómo se obtienen los dete. Otra de las propiedades fundamentales del determinante es que nos ayuda a detectar cuándo una matriz es invertible. esto nos permite agregar una equivalencia más a la lista de equivalencias de matrices invertibles que ya teníamos. teorema. una matriz a en m n (f) es invertible si y sólo si det a ≠ 0. demostración.

Solution Desvelando Las Propiedades De Los Determinantes Una Introducción Al álgebra Lineal Es como álgebra y probabilidad. .1.1. introducción a los determinanteslos determinantes están definidos pa. a matrices cuadradas, es decir, de nxn. el determinante de una. atriz cuadrada es un escalar (número). nos apoyaremos en las matrices de 2x2 para describir cómo se obtienen los dete. Otra de las propiedades fundamentales del determinante es que nos ayuda a detectar cuándo una matriz es invertible. esto nos permite agregar una equivalencia más a la lista de equivalencias de matrices invertibles que ya teníamos. teorema. una matriz a en m n (f) es invertible si y sólo si det a ≠ 0. demostración.

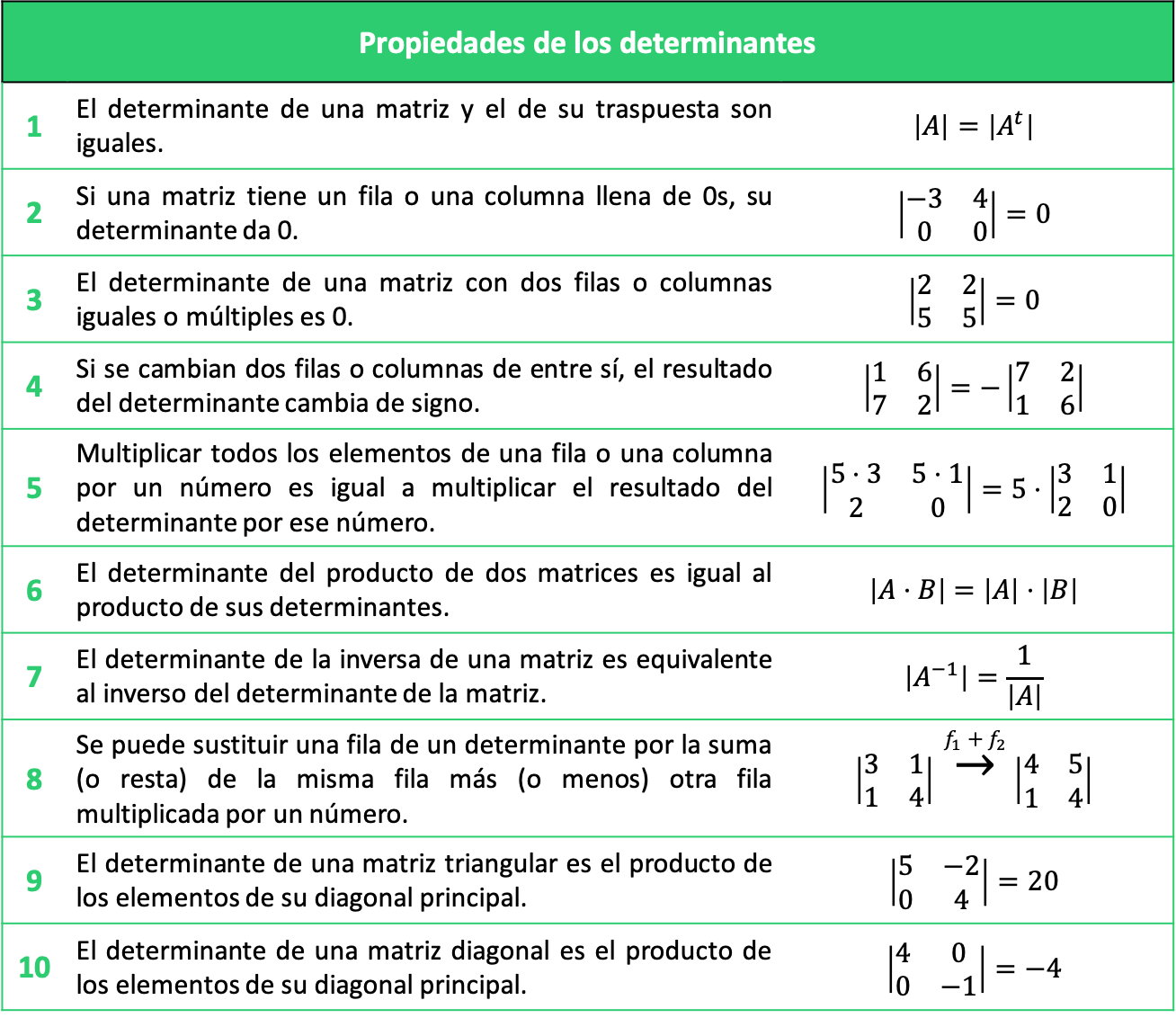
Todas Las Propiedades De Los Determinantes Con Ejercicios