Second Order Differential Equations Introduction Differentialequations Differentialequation

By hubloaded On Nov 7, 2024 Last updated

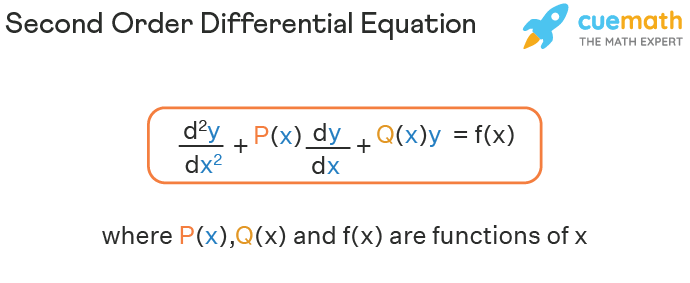
Second Order Differential Equation Solver Types Examples Methods Definition: characteristic equation. the characteristic equation of the second order differential equation ay'' by' cy=0 is. a\lambda^2 b\lambda c=0. \nonumber. the characteristic equation is very important in finding solutions to differential equations of this form. To solve a linear second order differential equation of the form. d 2 ydx 2 p dydx qy = 0. where p and q are constants, we must find the roots of the characteristic equation. r 2 pr q = 0. there are three cases, depending on the discriminant p 2 4q. when it is. positive we get two real roots, and the solution is. y = ae r 1 x be r 2 x.

2nd Order Differential Equations Teaching Resources 1. constant coefﬁcient second order linear odes we now proceed to study those second order linear equations which have constant coeﬃcients. the general form of such an equation is: a d2y dx2 b dy dx cy = f(x) (3) where a,b,c are constants. the homogeneous form of (3) is the case when f(x) ≡ 0: a d2y dx2 b dy dx cy = 0 (4). 17.1: second order linear equations we often want to find a function (or functions) that satisfies the differential equation. the technique we use to find these solutions varies, depending on the form of the differential equation with which we are working. second order differential equations have several important characteristics that can help. Second order constant coefficient differential equations can be used to model spring mass systems. an examination of the forces on a spring mass system results in a differential equation of the form \[mx″ bx′ kx=f(t), \nonumber \] where mm represents the mass, bb is the coefficient of the damping force, \(k\) is the spring constant, and \(f. Repeated roots – in this section we discuss the solution to homogeneous, linear, second order differential equations, ay′′ by′ cy = 0 a y ″ b y ′ c y = 0, in which the roots of the characteristic polynomial, ar2 br c = 0 a r 2 b r c = 0, are repeated, i.e. double, roots. we will use reduction of order to derive the second.

So, without further ado, let your Second Order Differential Equations Introduction Differentialequations Differentialequation journey unfold. Immerse yourself in the captivating realm of Second Order Differential Equations Introduction Differentialequations Differentialequation, and let your passion soar to new heights.

Second order Differential Equations - Introduction | #differentialequations #differentialequation

Second order Differential Equations - Introduction | #differentialequations #differentialequation Second-Order Differential Equations (Introduction) Differential equation introduction | First order differential equations | Khan Academy How to solve differential equations Second Order Linear Differential Equations SOLVING FIRST ORDER LINEAR DIFFERENTIAL EQUATIONS| EPISODE-5 | @alphamathematicalinstitute Differential Equations Introduction | Differential Calculus Basics #differentialequation Introduction to Second Order Differential Equations - Ordinary Differential Equations | Lecture 12 Differential equations, a tourist's guide | DE1 Separable First Order Differential Equations - Basic Introduction 2nd order linear homogeneous differential equations 1 | Khan Academy

Conclusion

Following an extensive investigation, one can see that content provides educational facts concerning Second Order Differential Equations Introduction Differentialequations Differentialequation. From beginning to end, the writer shows remarkable understanding related to the field. Particularly, the explanation about Y stands out as a highlight. Whats more, the composition is noteworthy in breaking down complex concepts in an easy-to-understand manner. To add to that, the essayist provides practical examples that bring the concepts to life. A further characteristic that distinguishes this content is the thorough investigation of multiple aspects related to Second Order Differential Equations Introduction Differentialequations Differentialequation. The commentators thoroughness certifies that visitors gain an all-encompassing awareness of the subject matter. Thanks for spending time on the composition. If theres anything else youd like to know, feel free to contact me through email. I am enthusiastic about your messages. In summing up, as you continue exploring, you will find a variety of linked write-ups that are helpful:Wishing you enjoyable reading!