Second Order Differential Equation Solver Types Examples Methods
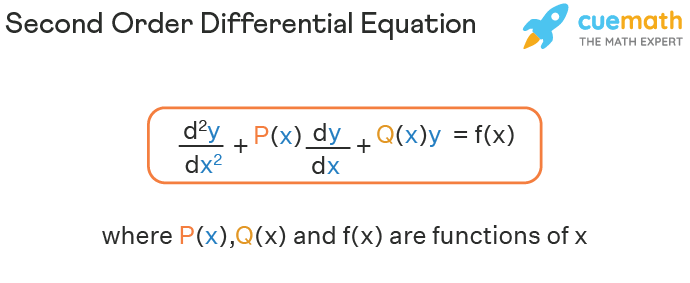
Second Order Differential Equation Solver Types Examples Methods Let us consider a few examples of each type to understand how to determine the solution of the homogeneous second order differential equation. example 1: solve the 2nd order differential equation y'' 6y' 5y = 0. solution: assume y = e rx and find its first and second derivative: y' = re rx, y'' = r 2 e rx. Definition: characteristic equation. the characteristic equation of the second order differential equation ay'' by' cy=0 is. a\lambda^2 b\lambda c=0. \nonumber. the characteristic equation is very important in finding solutions to differential equations of this form.

2nd Order Differential Equations Teaching Resources To solve a linear second order differential equation of the form. d 2 ydx 2 p dydx qy = 0. where p and q are constants, we must find the roots of the characteristic equation. r 2 pr q = 0. there are three cases, depending on the discriminant p 2 4q. when it is. positive we get two real roots, and the solution is. y = ae r 1 x be r 2 x. Resolution based on the types of solution of the characteristic equation $\boxed{a\lambda^2 b\lambda c=0}$, and by noting $\boxed{\delta=b^2 4ac}$ its discriminant, we distinguish the following cases:. Truncating this expansion at the rst order term in h we obtain the forward euler method: (12) u n 1 =u n hf(t n;u n): do not use the forward euler method unless there is no other choice. it is very inaccurate! truncating the series in (11) at the second order term we obtain the following second order taylor method which is hardly ever used: (13. Only first order ordinary differential equations of the form of equation \((\pageindex{1.1})\) can be solved by using the runge kutta 2nd order method. in other sections, we discuss how the euler and runge kutta methods are used to solve higher order ordinary or coupled (simultaneous) ordinary differential equations.

Solving Second Order Differential Equations Youtube Truncating this expansion at the rst order term in h we obtain the forward euler method: (12) u n 1 =u n hf(t n;u n): do not use the forward euler method unless there is no other choice. it is very inaccurate! truncating the series in (11) at the second order term we obtain the following second order taylor method which is hardly ever used: (13. Only first order ordinary differential equations of the form of equation \((\pageindex{1.1})\) can be solved by using the runge kutta 2nd order method. in other sections, we discuss how the euler and runge kutta methods are used to solve higher order ordinary or coupled (simultaneous) ordinary differential equations. We will have to find the “missing” solution of u(x) for a second order differential equation in equation (8.1) by following the procedure: let us try the following additional assumed form of the solution u(x) : u2(x) = v(x) emx (8.10) where v(x) is an assumed function of x, and it needs to be determined. We divide second order differential equations into two main types; a homogeneous second order differential equation is of the form where a, b and c are real constants; you may also see this written in the form where and a non homogeneous second order differential equation is of the form where a, b and c are real constants and where f(x) is a.

Chapter 8 Solving Second Order Differential Equations Numerically We will have to find the “missing” solution of u(x) for a second order differential equation in equation (8.1) by following the procedure: let us try the following additional assumed form of the solution u(x) : u2(x) = v(x) emx (8.10) where v(x) is an assumed function of x, and it needs to be determined. We divide second order differential equations into two main types; a homogeneous second order differential equation is of the form where a, b and c are real constants; you may also see this written in the form where and a non homogeneous second order differential equation is of the form where a, b and c are real constants and where f(x) is a.

Second Order Linear Differential Equations Youtube

Comments are closed.