Propiedades De Los Determinantes De Una Matriz Ejemplos Compartir Images

Mate Ii Integrales Propiedades De Los Determinantes Propiedad 1: determinante de la matriz transpuesta. 2. propiedad 2: determinante con una fila o columna llena de ceros. 3. propiedad 3: determinante con dos filas o columnas iguales. 4. propiedad 4: cambiar filas o columnas de un determinante. 5. propiedad 5: multiplicar una línea de una determinante por un escalar. Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):.

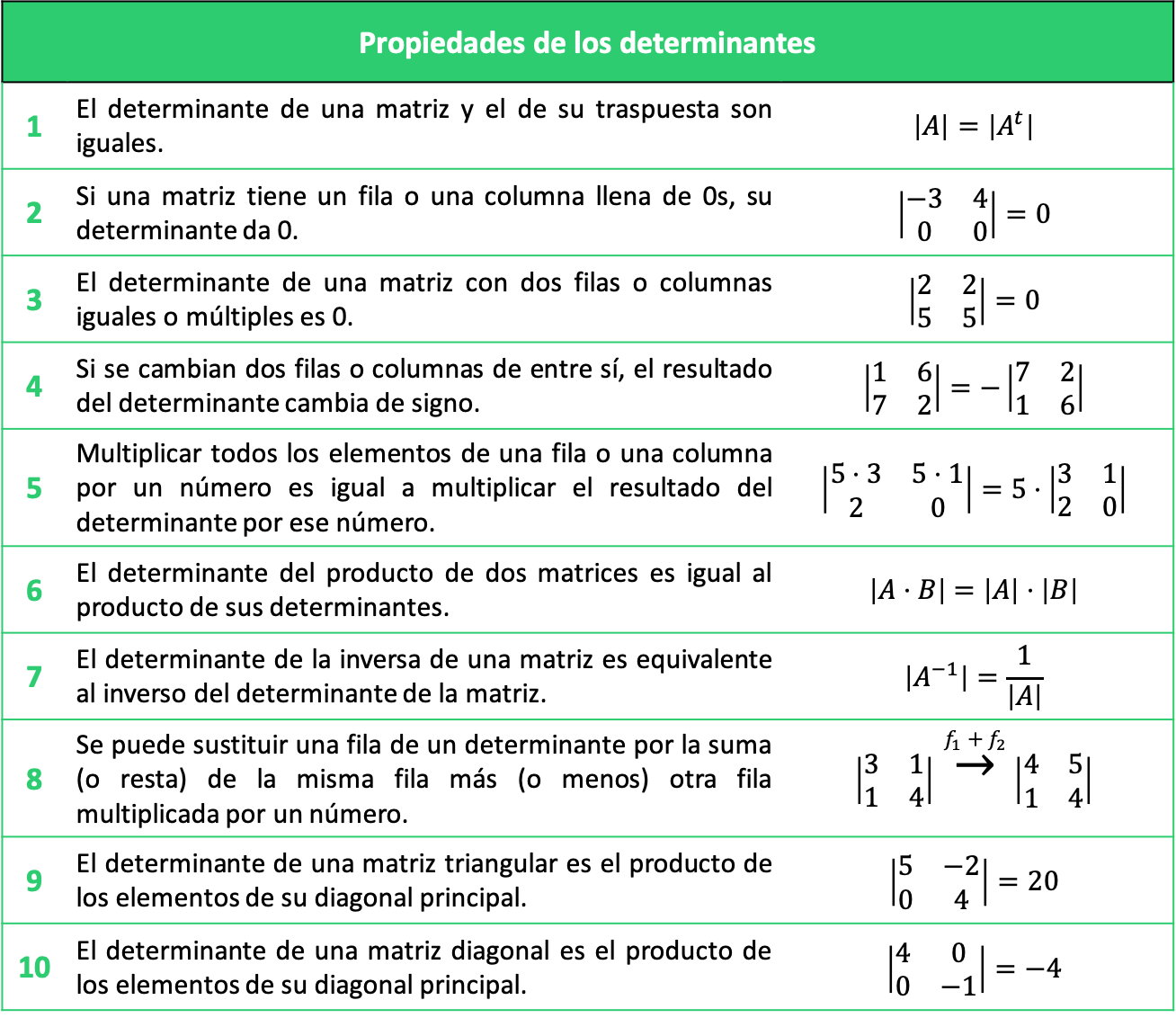
Todas Las Propiedades De Los Determinantes Con Ejercicios Propiedad 1. el determinante de una matriz cuadrada es igual al determinante de su traspuesta: por ejemplo: tenemos el siguiente determinante: lo resolvemos aplicando regla de sarrus: y operamos: ahora obtenemos su traspuesta: y volvemos a resolver el determinante: operamos y llegamos al mismo resultado:. Por lo tanto, cuando agregamos un múltiplo de una fila a otra fila, el determinante de la matriz no cambia. tenga en cuenta que si una matriz \(a\) contiene una fila que es un múltiplo de otra fila, \(\det \left(a\right)\) será igual \(0\). para ver esto, supongamos que la primera fila de \(a\) es igual a \( 1\) veces la segunda fila. Los determinantes tienen varias propiedades importantes que los hacen útiles en álgebra lineal y cálculo. a continuación se describen algunas de las propiedades más comunes: propiedad 1: el determinante de una matriz se mantiene igual si se intercambian filas o columnas. propiedad 2: el determinante de una matriz se multiplica por un. Los determinantes son funciones matemáticas que asignan un valor escalar a una matriz cuadrada y son fundamentales en el álgebra lineal. una propiedad esencial es que el determinante de una matriz es igual al de su matriz transpuesta, lo que significa que el determinante es invariante bajo la transposición de la matriz.

Propiedades De Los Determinantes De Una Matriz Ejemplos Compartir Images Los determinantes tienen varias propiedades importantes que los hacen útiles en álgebra lineal y cálculo. a continuación se describen algunas de las propiedades más comunes: propiedad 1: el determinante de una matriz se mantiene igual si se intercambian filas o columnas. propiedad 2: el determinante de una matriz se multiplica por un. Los determinantes son funciones matemáticas que asignan un valor escalar a una matriz cuadrada y son fundamentales en el álgebra lineal. una propiedad esencial es que el determinante de una matriz es igual al de su matriz transpuesta, lo que significa que el determinante es invariante bajo la transposición de la matriz. Las propiedades de los determinantes se aplican a matrices cuadradas de cualquier orden y facilitan el cálculo de los determinantes. propiedades generales. estas son algunas de las propiedades generales de los determinantes: el determinante de una matriz a a a y el de su traspuesta a t a^t a t son iguales. ∣ a t ∣ = ∣ a ∣ |a^t|=|a| ∣. Pues bien, para ello tenemos la fortuna de contar con algunas propiedades de determinantes, una de ellas es la siguiente: 1️⃣ propiedad 1: sean dos matrices a y b respectivamente de nxn, entonces. det ab = det a * det b. o sea que el determinante del producto de a y b es igual al producto de la determinante de a con b.

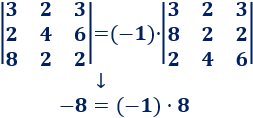
Propiedades De Los Determinantes De Matrices Con Ejemplos Las propiedades de los determinantes se aplican a matrices cuadradas de cualquier orden y facilitan el cálculo de los determinantes. propiedades generales. estas son algunas de las propiedades generales de los determinantes: el determinante de una matriz a a a y el de su traspuesta a t a^t a t son iguales. ∣ a t ∣ = ∣ a ∣ |a^t|=|a| ∣. Pues bien, para ello tenemos la fortuna de contar con algunas propiedades de determinantes, una de ellas es la siguiente: 1️⃣ propiedad 1: sean dos matrices a y b respectivamente de nxn, entonces. det ab = det a * det b. o sea que el determinante del producto de a y b es igual al producto de la determinante de a con b.