Propiedades De Los Determinantes De Matrices 03

Propiedades De Los Determinantes De Matrices 03 Youtube Propiedad 1: determinante de la matriz transpuesta. 2. propiedad 2: determinante con una fila o columna llena de ceros. 3. propiedad 3: determinante con dos filas o columnas iguales. 4. propiedad 4: cambiar filas o columnas de un determinante. 5. propiedad 5: multiplicar una línea de una determinante por un escalar. Usando la definición 3.1.1 podemos encontrar el determinante de la siguiente manera: det (a) = 3 × 4 − 2 × 6 = 12 − 12 = 0 por teorema no3.2.7a es invertible. ahora considere la matriz b. nuevamente por definición 3.1.1 tenemos det (b) = 2 × 1 − 5 × 3 = 2 − 15 = − 13 por teorema 3.2.7b es invertible y el determinante de la.

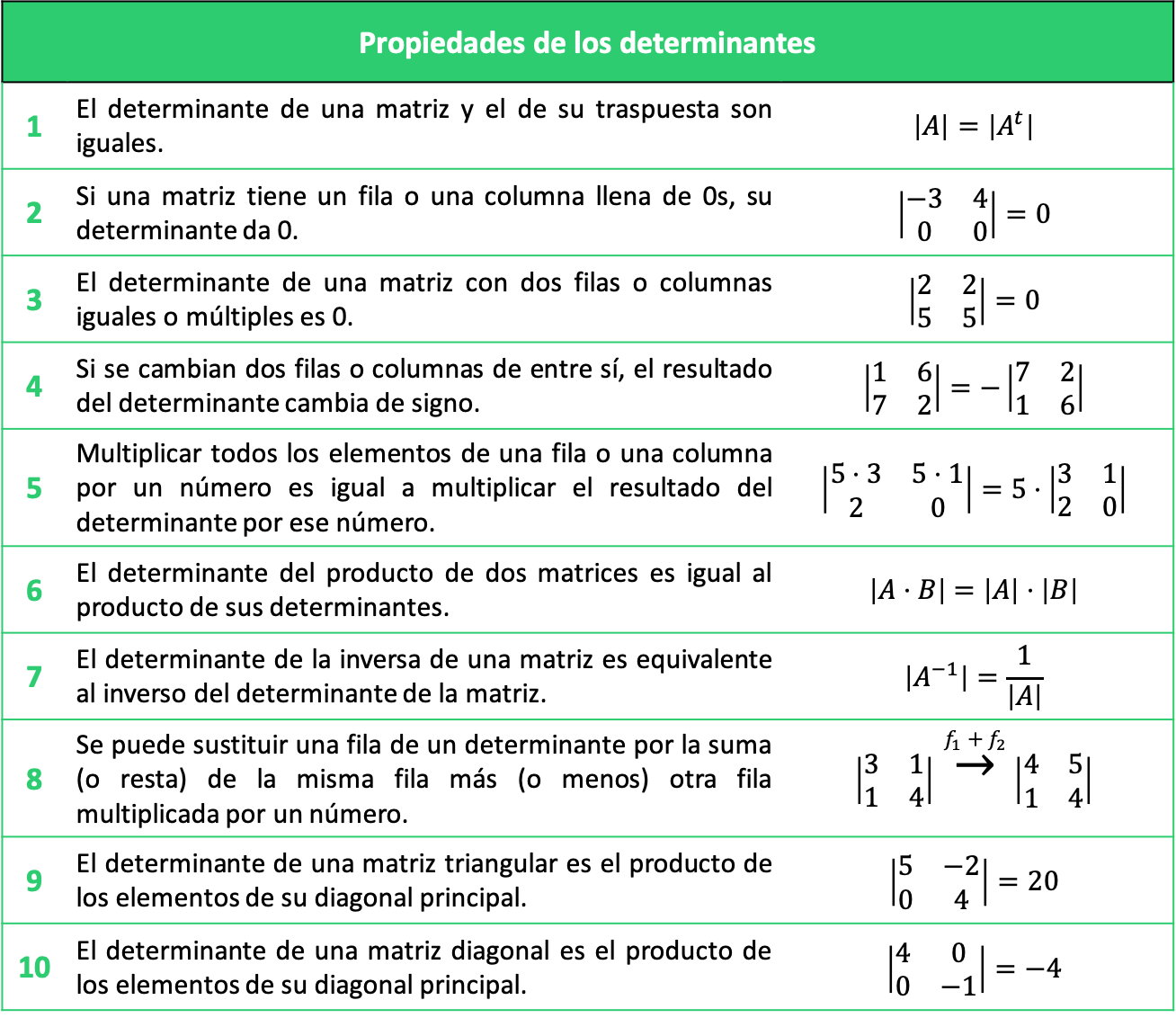
Todas Las Propiedades De Los Determinantes Con Ejercicios Correspondiente a 2º de bachillerato, en este vídeo se aplican las siguientes propiedades de los determinantes a un ejercicio concreto:1) si en un determinan. Propiedad 1. el determinante de una matriz cuadrada es igual al determinante de su traspuesta: por ejemplo: tenemos el siguiente determinante: lo resolvemos aplicando regla de sarrus: y operamos: ahora obtenemos su traspuesta: y volvemos a resolver el determinante: operamos y llegamos al mismo resultado:. Explicación con ejemplos de las propiedades de los determinantes, dentro del curso de matrices.curso completo de matrices: playlist?li. Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):.

Mate Ii Integrales Propiedades De Los Determinantes Explicación con ejemplos de las propiedades de los determinantes, dentro del curso de matrices.curso completo de matrices: playlist?li. Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):. 8.7 determinante de matrices libretexts español. 8.7 determinante de matrices. page id. 107418. un determinante es un número calculado a partir de las entradas en una matriz cuadrada. tiene muchas propiedades e interpretaciones que explorarás en álgebra lineal. este concepto se centra en el procedimiento de cálculo de determinantes. El determinante de una matriz proporciona información para responder a esta pregunta. cuando vimos producto vectorial y mixto, habíamos definido determinantes de orden 2 y de orden 3. recordamos aquí las fórmulas presentadas: a cada matriz cuadrada puede asignársele un número real que llamaremos su determinante y designaremos como \ (det.