Polar Curves Brilliant Math Science Wiki

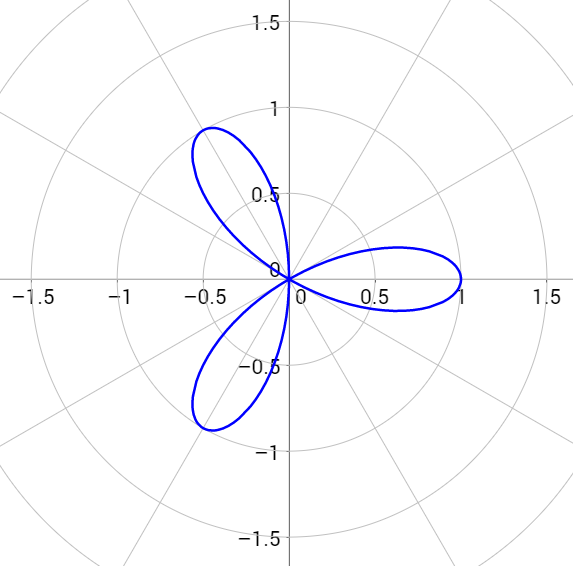
Polar Curves Brilliant Math Science Wiki Polar curves are defined by points that are a variable distance from the origin (the pole) depending on the angle measured off the positive x x axis. polar curves can describe familiar cartesian shapes such as ellipses as well as some unfamiliar shapes such as cardioids and lemniscates. r=1 \cos {\theta}\sin {3\theta} r = 1−cosθsin3θ. For instance the polar equation r = f (\theta) r = f (θ) describes a curve. the formula for the area under this polar curve is given by the formula below: consider the arc of the polar curve r = f (\theta) r = f (θ) traced as \theta θ varies from \theta 1 θ1 to \theta 2 θ2. if this arc bounds a closed region of the plane, the area of this.
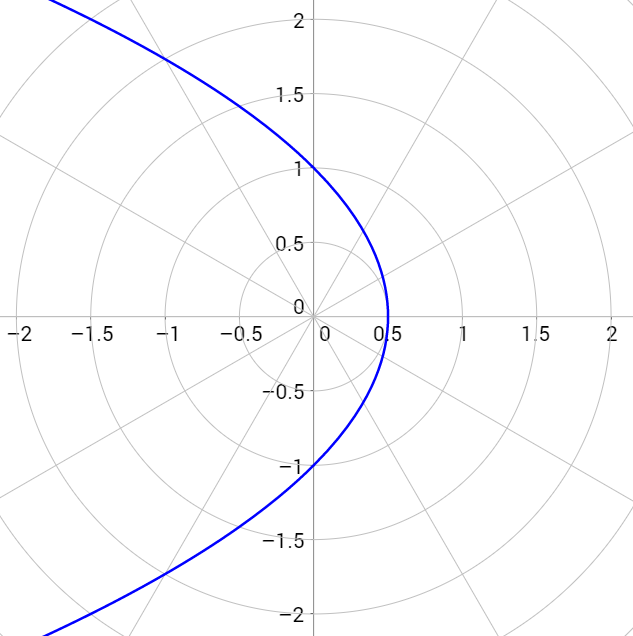
Polar Curves Brilliant Math Science Wiki Sometimes arclengths are found in the cartesian plane with rectangular (x,y) (x,y) coordinates. but it can also be calculated using polar coordinates. for instance the polar equation r = f (\theta) r = f (θ) describes a curve. the formula for the arclength of this polar curve is given by the formula below: if r = f (\theta) r = f (θ. 1. r = 3 sin 5 θ, r = 3 sin 2 θ r = 1 – 3 sin θ, r 2 = 25 sin 2 θ. the polar curves of these four polar equations are as shown below. match the polar equations with their corresponding polar curve. 2. test whether r 2 = 16 sin 2 θ is symmetric with respect to the polar axis, the line θ = θ 2, or the pole. 3. Hence the graph of the curve in polar coordinates is as follows: hence a circle is drawn. if were were to not restrict the domain to $[0, 2\pi]$ , then we would trace the circle out infinite times. To plot a polar curve, find points at increments of theta, then plot them on polar axes. r=3 3\sin {\theta} r=a\pm {a}\sin {\theta}, so it’s a cardioid through the origin. we’ll generate a table of values over the interval. with these points and knowing the shape of our polar curve, we can sketch the graph. 4 r=2 4\cos {\theta} r=a\pm {b.

Polar Curves Brilliant Math Science Wiki Hence the graph of the curve in polar coordinates is as follows: hence a circle is drawn. if were were to not restrict the domain to $[0, 2\pi]$ , then we would trace the circle out infinite times. To plot a polar curve, find points at increments of theta, then plot them on polar axes. r=3 3\sin {\theta} r=a\pm {a}\sin {\theta}, so it’s a cardioid through the origin. we’ll generate a table of values over the interval. with these points and knowing the shape of our polar curve, we can sketch the graph. 4 r=2 4\cos {\theta} r=a\pm {b. Derivatives for polar curves. we have thus far worked with polar curves, that is curves in the form r = f(θ). recall the translation equations for coordinates in the xy coordinate system to the polar coordinate system are as follows: (1) x = r cos θ y = r sin θ. hence it follows that x = f(θ) cos θ and y = f(θ) sin θ. Example 1. graph the polar curve defined by the equation r = θ on the interval [0, 2π] let's first graph some values to see what is happening with the polar coordinates: so as θ increases, the the distance away from the origin also increases on the entire interval [0, 2π]. hence, we obtain somewhat of a spiral that originates at the origin.

Polar Curves Brilliant Math Science Wiki Derivatives for polar curves. we have thus far worked with polar curves, that is curves in the form r = f(θ). recall the translation equations for coordinates in the xy coordinate system to the polar coordinate system are as follows: (1) x = r cos θ y = r sin θ. hence it follows that x = f(θ) cos θ and y = f(θ) sin θ. Example 1. graph the polar curve defined by the equation r = θ on the interval [0, 2π] let's first graph some values to see what is happening with the polar coordinates: so as θ increases, the the distance away from the origin also increases on the entire interval [0, 2π]. hence, we obtain somewhat of a spiral that originates at the origin.
Polar Curves Brilliant Math Science Wiki

Comments are closed.