More Examples Of Second Order Differential Equations

2nd Order Differential Equations Teaching Resources Second order differential equations. d2y dx2 p (x) dy dx q (x)y = f (x) undetermined coefficients which only works when f (x) is a polynomial, exponential, sine, cosine or a linear combination of those. variation of parameters which is a little messier but works on a wider range of functions. Definition: characteristic equation. the characteristic equation of the second order differential equation ay'' by' cy=0 is. a\lambda^2 b\lambda c=0. \nonumber. the characteristic equation is very important in finding solutions to differential equations of this form.

Second Order Linear Differential Equations Youtube Let us consider a few examples of each type to understand how to determine the solution of the homogeneous second order differential equation. example 1: solve the 2nd order differential equation y'' 6y' 5y = 0. solution: assume y = e rx and find its first and second derivative: y' = re rx, y'' = r 2 e rx. This video gives more examples of second order ordinary differential equations and their solutions. we review the characteristic polynomial and how to use i. Now, by newton’s second law, the sum of the forces on the system (gravity plus the restoring force) is equal to mass times acceleration, so we have. mx″ = − k(s x) mg = − ks − kx mg. however, by the way we have defined our equilibrium position, mg = ks, the differential equation becomes. mx″ kx = 0. 1. constant coefficient second order linear odes we now proceed to study those second order linear equations which have constant coefficients. the general form of such an equation is: a d2y dx2 b dy dx cy = f(x) (3) where a,b,c are constants. the homogeneous form of (3) is the case when f(x) ≡ 0: a d2y dx2 b dy dx cy = 0 (4).
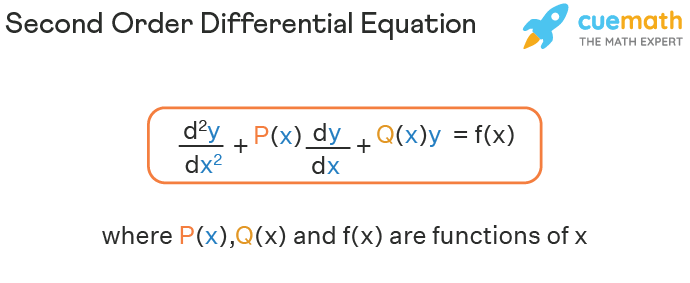
Second Order Differential Equation Solver Types Examples Methods Now, by newton’s second law, the sum of the forces on the system (gravity plus the restoring force) is equal to mass times acceleration, so we have. mx″ = − k(s x) mg = − ks − kx mg. however, by the way we have defined our equilibrium position, mg = ks, the differential equation becomes. mx″ kx = 0. 1. constant coefficient second order linear odes we now proceed to study those second order linear equations which have constant coefficients. the general form of such an equation is: a d2y dx2 b dy dx cy = f(x) (3) where a,b,c are constants. the homogeneous form of (3) is the case when f(x) ≡ 0: a d2y dx2 b dy dx cy = 0 (4). Repeated roots – in this section we discuss the solution to homogeneous, linear, second order differential equations, ay′′ by′ cy = 0 a y ″ b y ′ c y = 0, in which the roots of the characteristic polynomial, ar2 br c = 0 a r 2 b r c = 0, are repeated, i.e. double, roots. we will use reduction of order to derive the second. 19.3 second order differential equations. a second order differential equation is one that expresses the second derivative of the dependent variable as a function of the variable and its first derivative. (more generally it is an equation involving that variable and its second derivative, and perhaps its first derivative.).

Solving Second Order Differential Equations Youtube Repeated roots – in this section we discuss the solution to homogeneous, linear, second order differential equations, ay′′ by′ cy = 0 a y ″ b y ′ c y = 0, in which the roots of the characteristic polynomial, ar2 br c = 0 a r 2 b r c = 0, are repeated, i.e. double, roots. we will use reduction of order to derive the second. 19.3 second order differential equations. a second order differential equation is one that expresses the second derivative of the dependent variable as a function of the variable and its first derivative. (more generally it is an equation involving that variable and its second derivative, and perhaps its first derivative.).

Comments are closed.