Memahami Perbandingan Trigonometri Sudut Istimewa Varia Katadata Co Id

Memahami Perbandingan Trigonometri Sudut Istimewa Varia Katadata Co Id Memahami perbandingan trigonometri sudut istimewa. oleh destiara anggita putri. 10 agustus 2023, 08:30. pexels. ilustrasi, soal matematika. dalam mata pelajaran sma, siswa akan mempelajari materi trigonometri. ini suatu cabang ilmu matematika yang mempelajari mengenai sudut, sisi, dan perbandingan antara sudut terhadap sisi. Di antara sudut sudut segitiga, terdapat beberapa sudut istimewa dalam trigonometri, antara lain 0°, 30°, 45°, 60°, dan 90°. dikatakan istimewa, karena sudut ini memiliki nilai perbandingan trigonometri yang dapat diketahui dengan mudah tanpa menggunakan kalkulator. 1. tabel sin cos tan kuadran i. 0°: sin 0, cos 1, tan 0.

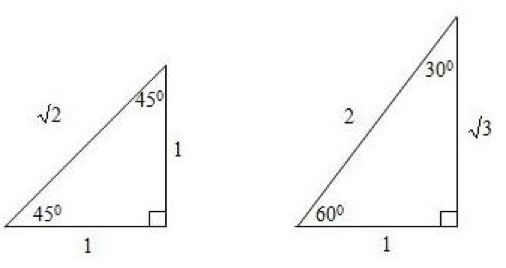
Memahami Perbandingan Trigonometri Sudut Istimewa Varia Katadata Co Id Sudut sudut istimewa antara lain 0°, 30°, 45°, 60°, dan 90°. adapun tabel sudut istimewa trigonometri yang bisa dipelajari, yaitu: 1. sudut istimewa trigonometri kuadran i. sumber: kumparan. berikut ini perbandingan trigonometri untuk sudut istimewa pada kuadran i: 0°: sin 0, cos 1, tan 0. Dalam kasus ini, sudut tajam 60 derajat adalah sudut istimewa trigonometri. anggap tinggi atap tersebut sebagai h. anda dapat menggunakan trigonometri untuk mencari tinggi atap dengan memanfaatkan sudut 60 derajat dan panjang alas 12 meter. tinggi atap panjang alas atap = tangen 60° h 12 = √3. h = 12 × √3. h ≈ 20.78 meter. Katadata menyediakan berita, riset, analisis seputar perbandingan trigonometri sudut istimewa terbaru dan terkini. Berikut ini contoh soal trigonometri untuk memahaminya lebih mudah. 1. diketahui panjang sisi miring sebuah segitiga adalah 10 cm dan sudut yang terbentuk adalah 30 derajat. hitunglah panjang sisi yang sejajar dengan sudut tersebut! jawab: sisi yang sejajar dengan sudut 30 derajat adalah sin (30) = 1 2 x sisi miring.

Memahami Perbandingan Trigonometri Sudut Istimewa Varia Katadata Co Id Katadata menyediakan berita, riset, analisis seputar perbandingan trigonometri sudut istimewa terbaru dan terkini. Berikut ini contoh soal trigonometri untuk memahaminya lebih mudah. 1. diketahui panjang sisi miring sebuah segitiga adalah 10 cm dan sudut yang terbentuk adalah 30 derajat. hitunglah panjang sisi yang sejajar dengan sudut tersebut! jawab: sisi yang sejajar dengan sudut 30 derajat adalah sin (30) = 1 2 x sisi miring. Misalnya sudut 0°, 30°, 45°, 60°, dan 90° merupakan sudut sudut istimewa di kuadran i. untuk kuadran ii, sudut istimewanya ada 120°, 135°, 150°, 180°. sudut istimewa pada kuadran iii ada 210°, 225°, 240°, dan 270°. sedangkan di kuadran iv 300°, 315°, 330°, dan 360°. bagaimana cara menentukan nilai perbandingan trigonometri. C. nilai perbandingan trigonometri untuk sudut 30 ∘. perhatikan gambar berikut! segitiga poq adalah segitiga sama sisi dengan op = oq = pq = 1. ∠ p o q = ∠ o q p = ∠ o p q = 60 ∘. ∠ p o q = 60 ∘ 2 α = 60 ∘ α = 30 ∘. titik p’ adalah titik tengah pq maka p p ′ = 1 2 , diperoleh ordinat titik p adalah 1 2.

Perbandingan Trigonometri Sudut Istimewa Sinau Matematika Misalnya sudut 0°, 30°, 45°, 60°, dan 90° merupakan sudut sudut istimewa di kuadran i. untuk kuadran ii, sudut istimewanya ada 120°, 135°, 150°, 180°. sudut istimewa pada kuadran iii ada 210°, 225°, 240°, dan 270°. sedangkan di kuadran iv 300°, 315°, 330°, dan 360°. bagaimana cara menentukan nilai perbandingan trigonometri. C. nilai perbandingan trigonometri untuk sudut 30 ∘. perhatikan gambar berikut! segitiga poq adalah segitiga sama sisi dengan op = oq = pq = 1. ∠ p o q = ∠ o q p = ∠ o p q = 60 ∘. ∠ p o q = 60 ∘ 2 α = 60 ∘ α = 30 ∘. titik p’ adalah titik tengah pq maka p p ′ = 1 2 , diperoleh ordinat titik p adalah 1 2.

Memahami Perbandingan Trigonometri Sudut Istimewa Varia Katadata Co Id