Matrix Algebra Matrix Multiplication Matrices Algebra Subtraction

Matrix Algebra Matrix Multiplication Matrices Algebra Subtraction Matrices are the arrangement of numbers or any other mathematical elements in the form of rectangular arrays. algebra of matrices denotes the various algebraic operations performed on a matrix. algebra of matrices includes operations such as addition, subtraction, multiplication, transpose, negative, and determinant of the matrix. It is a special matrix, because when we multiply by it, the original is unchanged: a × i = a. i × a = a. order of multiplication. in arithmetic we are used to: 3 × 5 = 5 × 3 (the commutative law of multiplication) but this is not generally true for matrices (matrix multiplication is not commutative): ab ≠ ba.

Subtraction Of Two Matrices Matrix Subtraction Subtract Matrices To add two matrices: add the numbers in the matching positions: these are the calculations: 3 4=7. 8 0=8. 4 1=5. 6−9=−3. the two matrices must be the same size, i.e. the rows must match in size, and the columns must match in size. example: a matrix with 3 rows and 5 columns can be added to another matrix of 3 rows and 5 columns. Finding scalar multiples of a matrix. besides adding and subtracting whole matrices, there are many situations in which we need to multiply a matrix by a constant called a scalar. recall that a scalar is a real number quantity that has magnitude, but not direction. for example, time, temperature, and distance are scalar quantities. A row in a matrix is a set of numbers that are aligned horizontally. a column in a matrix is a set of numbers that are aligned vertically. each number is an entry, sometimes called an element, of the matrix. matrices (plural) are enclosed in [ ] or ( ), and are usually named with capital letters. for example, three matrices named a, b, and c. The resultant matrix obtained by multiplication of two matrices, is the order of m 1, n 2, where m 1 is the number of rows in the 1st matrix and n 2 is the number of column of the 2nd matrix. rule of matrix algebra. the algebra of matrix follows some rules for addition and multiplication. let us consider a, b and c are three different square.
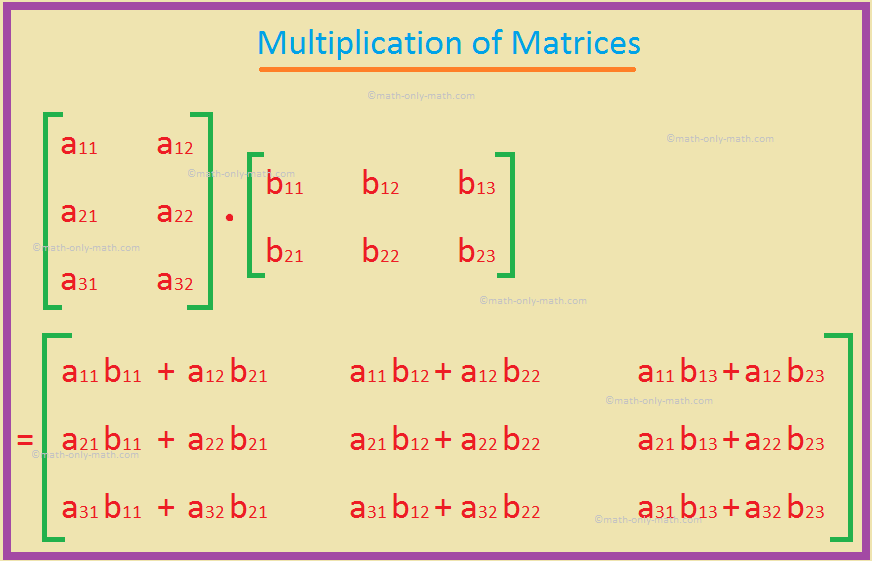
Multiplication Of Matrices How To Multiply Matrices Rules Examples A row in a matrix is a set of numbers that are aligned horizontally. a column in a matrix is a set of numbers that are aligned vertically. each number is an entry, sometimes called an element, of the matrix. matrices (plural) are enclosed in [ ] or ( ), and are usually named with capital letters. for example, three matrices named a, b, and c. The resultant matrix obtained by multiplication of two matrices, is the order of m 1, n 2, where m 1 is the number of rows in the 1st matrix and n 2 is the number of column of the 2nd matrix. rule of matrix algebra. the algebra of matrix follows some rules for addition and multiplication. let us consider a, b and c are three different square. The matrices that appear are real or complex numbers. addition and subtraction of matrices and multiplication of a matrix by a scalar addition and subtraction of matrices is defined only for matrices with the same dimen sions. we begin with addition. definition 2.2.1 if a and b are both m×n matrices, then we define addition (or the sum)ofa and. Therefore, in multiplication of matrices, it is useful to distinguish between pre and post multiplication of one matrix by another. in the matrix multiplication ab = c, we say that b is pre multiplied by a or that a is post multiplied by b to form matrix c. once the conformability for multiplication is established, the element in a given row and.
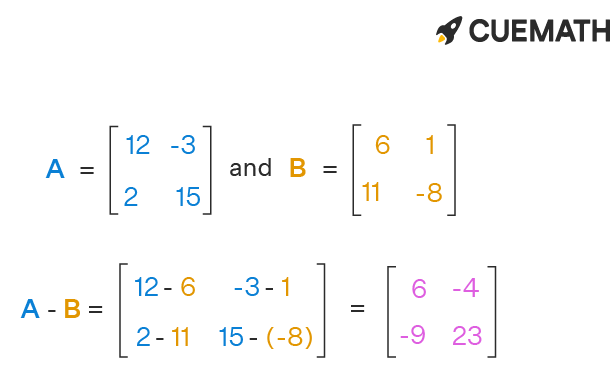
Subtraction Of Matrices Properties What Is Matrix Subtraction The matrices that appear are real or complex numbers. addition and subtraction of matrices and multiplication of a matrix by a scalar addition and subtraction of matrices is defined only for matrices with the same dimen sions. we begin with addition. definition 2.2.1 if a and b are both m×n matrices, then we define addition (or the sum)ofa and. Therefore, in multiplication of matrices, it is useful to distinguish between pre and post multiplication of one matrix by another. in the matrix multiplication ab = c, we say that b is pre multiplied by a or that a is post multiplied by b to form matrix c. once the conformability for multiplication is established, the element in a given row and.

Comments are closed.