Linear Algebra Let A Be The Matrix A And A Find A Basis For The Row Space Of A Studyx

Finding Basis For The Row Space Of A Matrix Linear Algebra Youtube Rref(a) = [1 0 9 2 0 1 − 3 1 0 0 0 0]. (a) find a basis for the nullspace of a. by the computation above, we see that the general solution of ax = 0 is. x1 = − 9x3 − 2x4 x2 = 3x3 − x4, where x3 and x4 are free variables. thus, the vector form solution to ax = 0 is. x = [x1 x2 x3 x4] = [− 9x3 − 2x4 3x3 − x4 x3 x4] = x3[− 9 3 1 0. Let a be an m by n matrix. the space spanned by the rows of a is called the row space of a, denoted rs (a); it is a subspace of r n . the space spanned by the columns of a is called the column space of a, denoted cs (a); it is a subspace of r m . the collection { r 1, r 2, …, r m } consisting of the rows of a may not form a basis for rs (a.

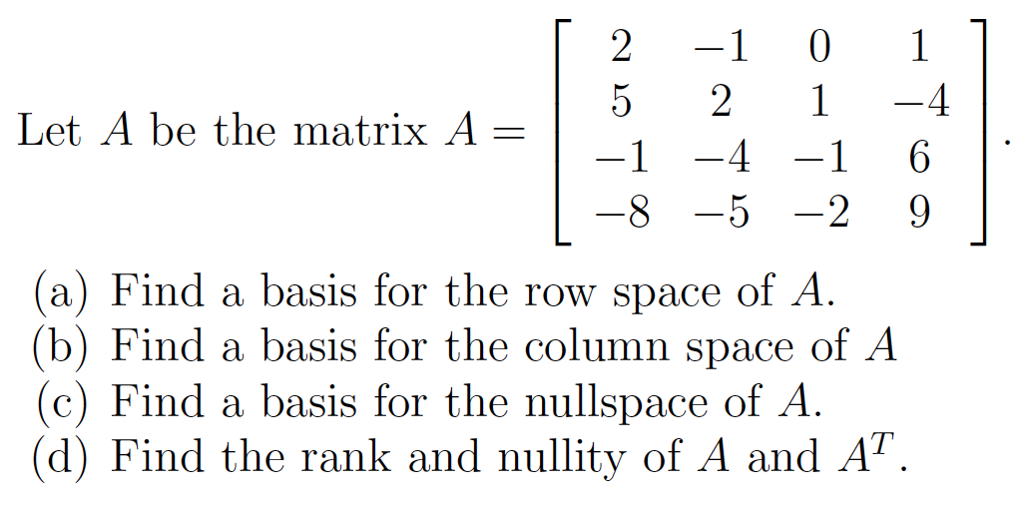
Linear Algebra Let A Be The Matrix A And A Find A Basis For The Row Space Of A Studyx The above theorem is referring to the pivot columns in the original matrix, not its reduced row echelon form. indeed, a matrix and its reduced row echelon form generally have different column spaces. for example, in the matrix \(a\) below: figure \(\pageindex{4}\) the pivot columns are the first two columns, so a basis for \(\text{col}(a)\) is. Question: linear algebra: let a be the matrix a, and (a) find a basis for the row space of a. (b) find a basis for the column space of a. (c) find a basis for the nullspace of a. (d) find the rank and nullity of a and a^t. The row space. as the columns of at are simply the rows of a we call ra(at) the row space of at. more precisely. definition: row space. the row space of the m by n matrix a is simply the span of its rows, i.e., ra(at) ≡ {aty|y ∈ rm} this is a subspace of rn. let us examine the matrix:. Linear algebra [1] 5.2 rank of matrix • row space and column space let a be an m×n matrix. – the row space of a = the span of rows of a ⊂ fn = rowa – the column space of a = the span of columns of a ⊂ fm = cola thm. a : m×n, u : p×m, v : n×q 1. col(av) ⊂ cola. if v is invertible, col(av) = cola. 2. row(ua) ⊂ rowa.

Linear Algebra 21 Basis For Row Space Youtube The row space. as the columns of at are simply the rows of a we call ra(at) the row space of at. more precisely. definition: row space. the row space of the m by n matrix a is simply the span of its rows, i.e., ra(at) ≡ {aty|y ∈ rm} this is a subspace of rn. let us examine the matrix:. Linear algebra [1] 5.2 rank of matrix • row space and column space let a be an m×n matrix. – the row space of a = the span of rows of a ⊂ fn = rowa – the column space of a = the span of columns of a ⊂ fm = cola thm. a : m×n, u : p×m, v : n×q 1. col(av) ⊂ cola. if v is invertible, col(av) = cola. 2. row(ua) ⊂ rowa. Reduce to row echelon form. the rows with leading 1's will be the basis vectors for the row space. when looking for the basis of the column space (given some matrix a), is the following method correct? reduce to row echelon form. the columns with leading 1's corresponding to the original matrix a will be the basis vectors for the column space. Rref(a) = [1 0 9 2 0 1 − 3 1 0 0 0 0]. (a) find a basis for the nullspace of a. by the computation above, we see that the general solution of ax = 0 is. x1 = − 9x3 − 2x4 x2 = 3x3 − x4, where x3 and x4 are free variables. thus, the vector form solution to ax = 0 is. x = [x1 x2 x3 x4] = [− 9x3 − 2x4 3x3 − x4 x3 x4] = x3[− 9 3 1 0.