Geometry Points Use Soh Cah Toa To Find Cos

Geometry Points Use Soh Cah Toa To Find Cos Youtube It’s a mnemonic device to help you remember the three basic trig ratios used to solve for missing sides and angles in a right triangle. it’s defined as: soh: sin (θ) = opposite hypotenuse. cah: cos (θ) = adjacent hypotenuse. toa: tan (θ) = opposite adjacent. Please subscribe: channel uchkkyp6ezvqq5kunzva mlg?sub confirmation=1to use soh cah toa to write the ratios for sine, cosine, and tan.

Geometry Points Use Soh Cah Toa To Write Sin Cos And Tan As A Decimal Youtube Sine, cosine and tangent. and sine, cosine and tangent are the three main functions in trigonometry. they are often shortened to sin, cos and tan. the calculation is simply one side of a right angled triangle divided by another side we just have to know which sides, and that is where "sohcahtoa" helps. We can use trigonometry to work out the unknown sides of a right angled triangle by using sohcahtoa. label the sides of the right angled triangle that we have information about. choose the trig ratio we need. substitute the values from the triangle into the function. calculate the unknown side, rearranging if necessary. We can use sohcahtoa if we know one side and one angle other than the right angle. given the first case where we know two sides, it is also possible to find the third side of the triangle using the pythagorean theorem, a 2 b 2 = c 2. in the case of a right triangle we can replace the variables a, b, and c with o, a, and h (o and a can be. Example. find the size of angle a°. step 1 the two sides we know are a djacent (6,750) and h ypotenuse (8,100). step 2 soh cah toa tells us we must use c osine. step 3 calculate adjacent hypotenuse = 6,750 8,100 = 0.8333. step 4 find the angle from your calculator using cos 1 of 0.8333: cos a° = 6,750 8,100 = 0.8333.

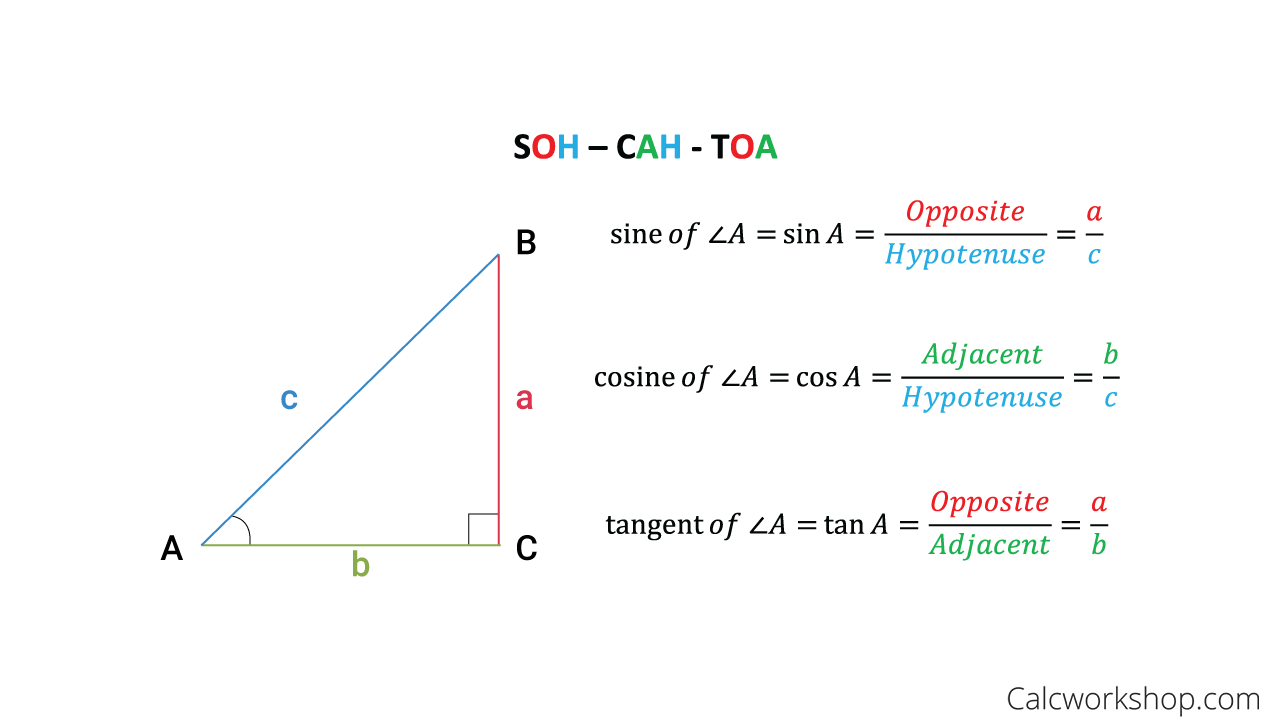
Soh Cah Toa Mnemonic We can use sohcahtoa if we know one side and one angle other than the right angle. given the first case where we know two sides, it is also possible to find the third side of the triangle using the pythagorean theorem, a 2 b 2 = c 2. in the case of a right triangle we can replace the variables a, b, and c with o, a, and h (o and a can be. Example. find the size of angle a°. step 1 the two sides we know are a djacent (6,750) and h ypotenuse (8,100). step 2 soh cah toa tells us we must use c osine. step 3 calculate adjacent hypotenuse = 6,750 8,100 = 0.8333. step 4 find the angle from your calculator using cos 1 of 0.8333: cos a° = 6,750 8,100 = 0.8333. A basic introduction to defining the three major trigonometric functions (sine, cosine, tangent) are discussed using the mnemonic soh cah toa. a review of basic trigonometry: sine, cosine & tangent including how to use the ratios to find missing sides and missing angles on right triangles. students learn that the sine of an angle of a right. Step 1: illustrate the situation to understand the problem. step 2: say, the angle from the cat’s point of view is denoted by ∠c. hence, we can note that the adjacent side measures 10 ft. and the opposite side measures 15 ft. in reference to ∠c. step 3: use the formula of toa. $\tan \theta =\frac {o} {a}$.

Soh Cah Toa Graphs Math Igcse A basic introduction to defining the three major trigonometric functions (sine, cosine, tangent) are discussed using the mnemonic soh cah toa. a review of basic trigonometry: sine, cosine & tangent including how to use the ratios to find missing sides and missing angles on right triangles. students learn that the sine of an angle of a right. Step 1: illustrate the situation to understand the problem. step 2: say, the angle from the cat’s point of view is denoted by ∠c. hence, we can note that the adjacent side measures 10 ft. and the opposite side measures 15 ft. in reference to ∠c. step 3: use the formula of toa. $\tan \theta =\frac {o} {a}$.