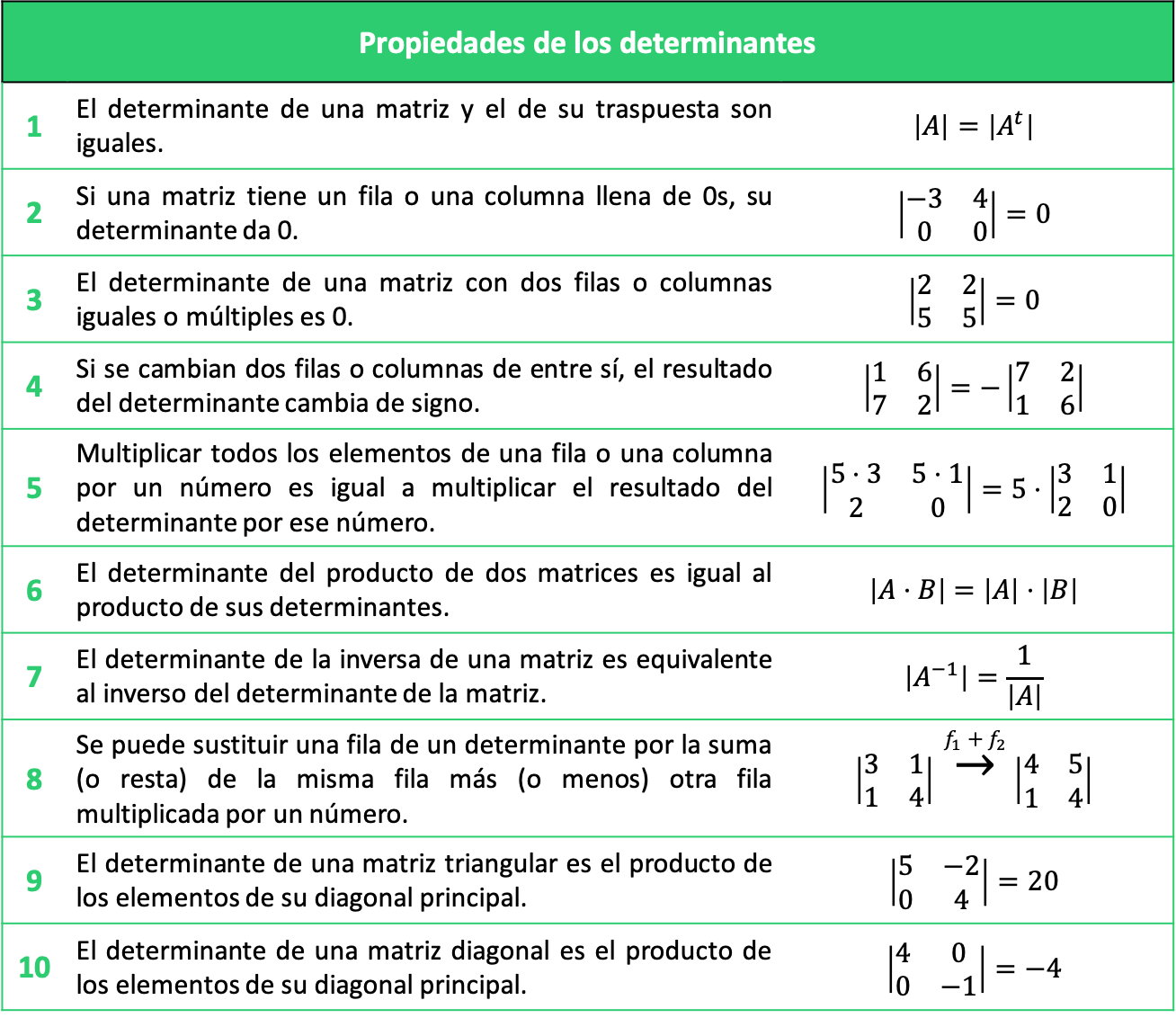
Todas Las Propiedades De Los Determinantes Con Ejercicios Propiedad 1: determinante de la matriz transpuesta. 2. propiedad 2: determinante con una fila o columna llena de ceros. 3. propiedad 3: determinante con dos filas o columnas iguales. 4. propiedad 4: cambiar filas o columnas de un determinante. 5. propiedad 5: multiplicar una línea de una determinante por un escalar. 0 2 = 0 . − 3 8 1 − 3 0 1. → estos determinantes no se hacen; se igualan directamente a 0, indicando el motivo. 2) un determinante vale 0 si tiene dos filas (o dos columnas) iguales o proporcionales. 3) un determinante vale 0 si una fila o columna es combinación lineal de otras.
Propiedades De Los Determinantes Youtube Usando la definición 3.1.1 podemos encontrar el determinante de la siguiente manera: det (a) = 3 × 4 − 2 × 6 = 12 − 12 = 0 por teorema no3.2.7a es invertible. ahora considere la matriz b. nuevamente por definición 3.1.1 tenemos det (b) = 2 × 1 − 5 × 3 = 2 − 15 = − 13 por teorema 3.2.7b es invertible y el determinante de la. Ejercicios resueltos paso a paso. en esta lección vamos a ver las propiedades de los determinantes. las propiedades de los determinantes nos permiten calcular un determinante sin necesidad de desarrollarlo, lo cual es especialmente útil en determinantes cuyos elementos sean letras o que su desarrollo sea algo complejo. 2 propiedades generales de los determinantes. 2.1 propiedad de multilinealidad. 2.2 propiedad de antisimetría. 2.3 propiedad de la identidad. 2.4 propiedad de los determinantes de matrices triangular. 2.5 propiedad de multiplicación de matrices. 3 aplicaciones de los determinantes en la matemática. 4 ejemplos de determinantes en distintas. Expandir contraer ubicación global. 17.2: propiedades de los determinantes. page id. dirk colbry. michigan state university. las siguientes son algunas propiedades útiles cuando se trabaja con determinantes. estas propiedades se utilizan a menudo en pruebas y a veces se pueden utilizar para hacer cálculos más rápidos.
Solution Desvelando Las Propiedades De Los Determinantes Una Introducción Al álgebra Lineal 2 propiedades generales de los determinantes. 2.1 propiedad de multilinealidad. 2.2 propiedad de antisimetría. 2.3 propiedad de la identidad. 2.4 propiedad de los determinantes de matrices triangular. 2.5 propiedad de multiplicación de matrices. 3 aplicaciones de los determinantes en la matemática. 4 ejemplos de determinantes en distintas. Expandir contraer ubicación global. 17.2: propiedades de los determinantes. page id. dirk colbry. michigan state university. las siguientes son algunas propiedades útiles cuando se trabaja con determinantes. estas propiedades se utilizan a menudo en pruebas y a veces se pueden utilizar para hacer cálculos más rápidos. Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):. Pues bien, para ello tenemos la fortuna de contar con algunas propiedades de determinantes, una de ellas es la siguiente: 1️⃣ propiedad 1: sean dos matrices a y b respectivamente de nxn, entonces. det ab = det a * det b. o sea que el determinante del producto de a y b es igual al producto de la determinante de a con b.
Determinantes En álgebra Lineal Todo Lo Que Necesitas Saber Cfn Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):. Pues bien, para ello tenemos la fortuna de contar con algunas propiedades de determinantes, una de ellas es la siguiente: 1️⃣ propiedad 1: sean dos matrices a y b respectivamente de nxn, entonces. det ab = det a * det b. o sea que el determinante del producto de a y b es igual al producto de la determinante de a con b.
Comments are closed.