Calculo De Determinantes Y Sus Propiedades Algebra Algebra Lineal Determinante De Una Matriz

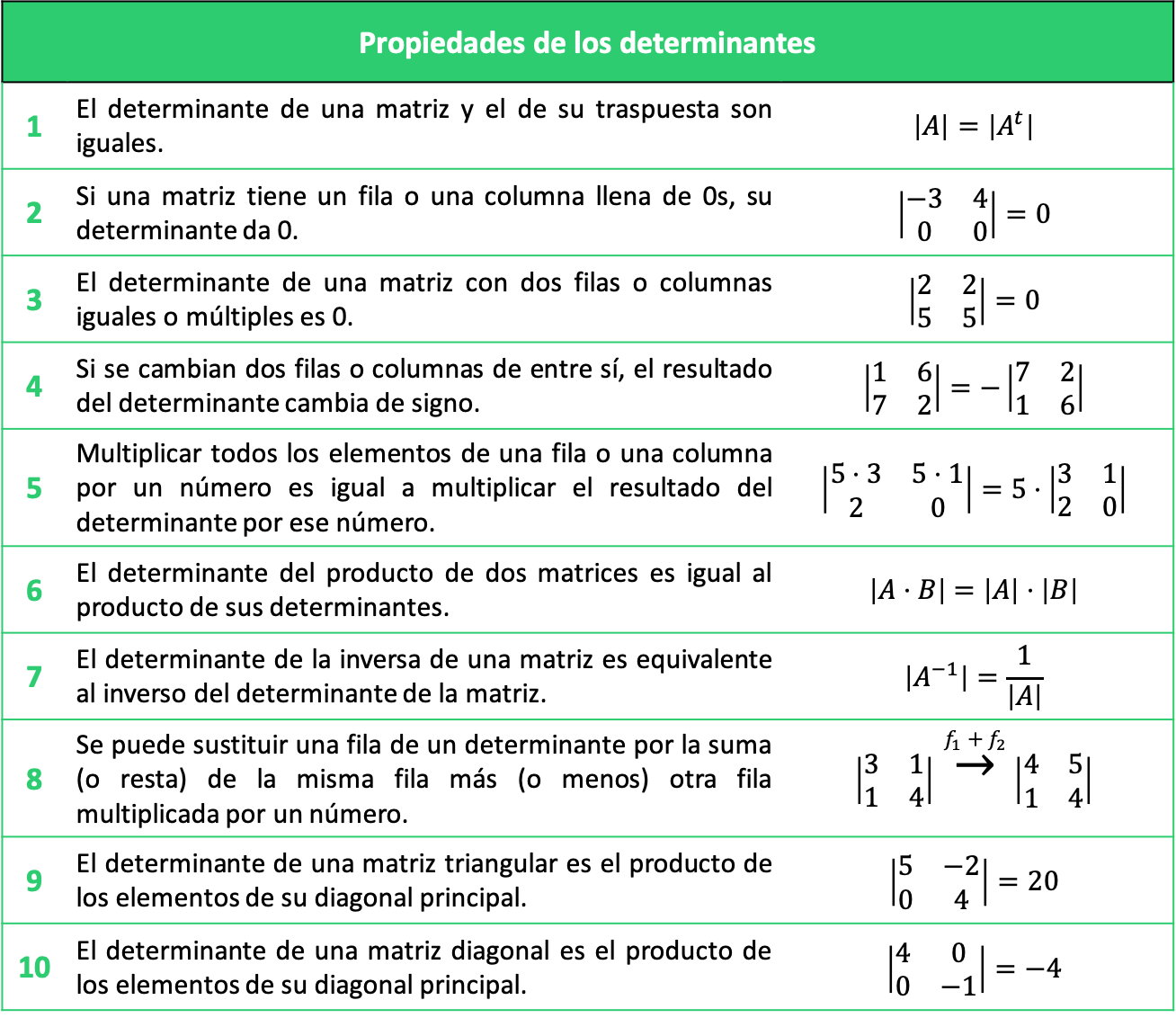
Todas Las Propiedades De Los Determinantes Con Ejercicios Propiedad 1: determinante de la matriz transpuesta. 2. propiedad 2: determinante con una fila o columna llena de ceros. 3. propiedad 3: determinante con dos filas o columnas iguales. 4. propiedad 4: cambiar filas o columnas de un determinante. 5. propiedad 5: multiplicar una línea de una determinante por un escalar. Propiedades básicas de los determinantes. las propiedades de los determinantes son cruciales para realizar cálculos eficientes y comprender el comportamiento de las matrices. a continuación, se enumeran algunas de las más importantes: determinante de la matriz identidad: el determinante de la matriz identidad es 1, es decir, det (i) = 1.

Cálculo De Determinantes Y Sus Propiedades álgebra Algebra Lineal Determinante De Una Matriz El determinante es una función. det: {square matrices} → r. satisfaciendo las siguientes propiedades: hacer un reemplazo de fila en a no cambia det (a). escalar una fila de a por un escalar c multiplica el determinante por c. el intercambio de dos filas de una matriz multiplica el determinante por − 1. Los determinantes tienen varias propiedades importantes que los hacen útiles en álgebra lineal y cálculo. a continuación se describen algunas de las propiedades más comunes: propiedad 1: el determinante de una matriz se mantiene igual si se intercambian filas o columnas. propiedad 2: el determinante de una matriz se multiplica por un. 32 el determinante de la matriz que resulta después de eliminar una fila y columna de una matriz cuadrada. this page titled 3.6: determinantes y regla de cramer is shared under a cc by nc sa 3.0 license and was authored, remixed, and or curated by anonymous via source content that was edited to the style and standards of the libretexts platform. Otra de las propiedades fundamentales del determinante es que nos ayuda a detectar cuándo una matriz es invertible. esto nos permite agregar una equivalencia más a la lista de equivalencias de matrices invertibles que ya teníamos. teorema. una matriz a en m n (f) es invertible si y sólo si det a ≠ 0. demostración.

Determinante De Una Matriz 2x2 álgebra Lineal Youtube 32 el determinante de la matriz que resulta después de eliminar una fila y columna de una matriz cuadrada. this page titled 3.6: determinantes y regla de cramer is shared under a cc by nc sa 3.0 license and was authored, remixed, and or curated by anonymous via source content that was edited to the style and standards of the libretexts platform. Otra de las propiedades fundamentales del determinante es que nos ayuda a detectar cuándo una matriz es invertible. esto nos permite agregar una equivalencia más a la lista de equivalencias de matrices invertibles que ya teníamos. teorema. una matriz a en m n (f) es invertible si y sólo si det a ≠ 0. demostración. Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):. Es como álgebra y probabilidad. .1.1. introducción a los determinanteslos determinantes están definidos pa. a matrices cuadradas, es decir, de nxn. el determinante de una. atriz cuadrada es un escalar (número). nos apoyaremos en las matrices de 2x2 para describir cómo se obtienen los dete.