Area Y Perimetro De Un Triangulo Rectangulo Ejemplo 1

área Y Perímetro De Un Triángulo Rectángulo Ejemplo 1 Youtube El perímetro de un triángulo puede ser encontrado al sumar las longitudes de sus tres lados y su área puede ser encontrada al multiplicar por un medio al producto de su base y de su altura. a continuación, aprenderemos todo lo relacionado con el perímetro y el área de triángulos. About press copyright contact us creators advertise developers terms privacy policy & safety how works test new features nfl sunday ticket press copyright.

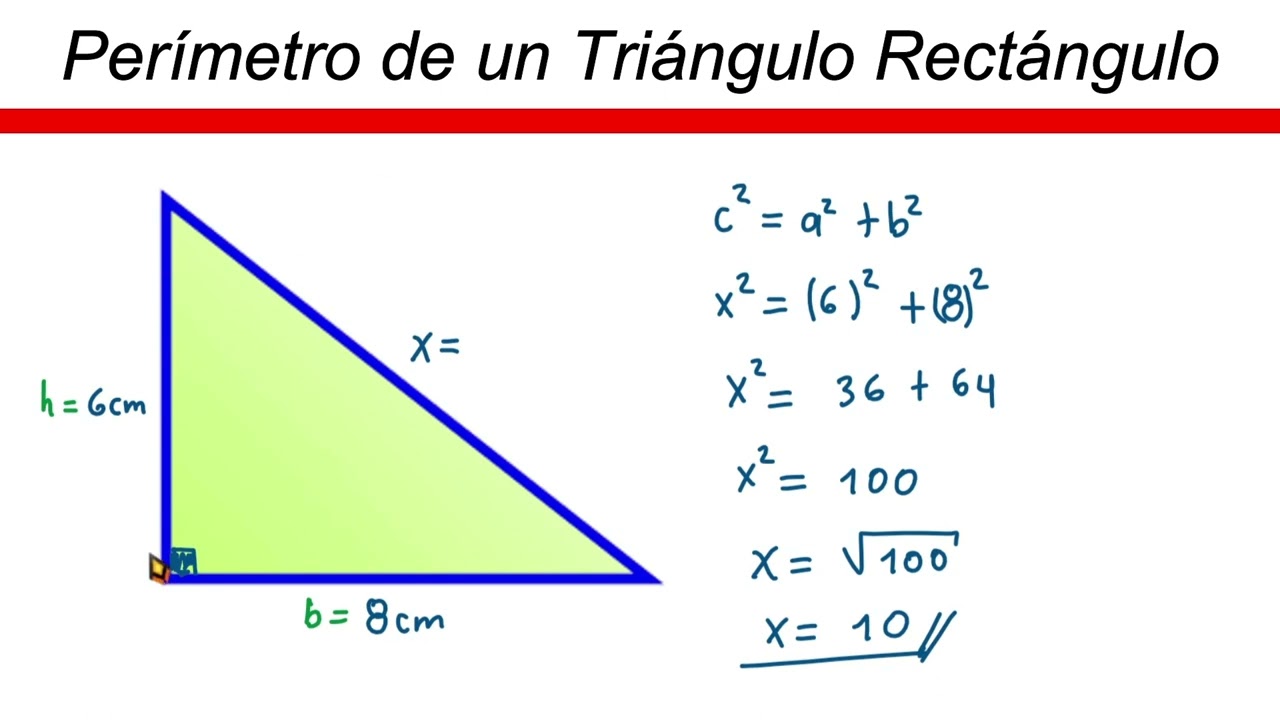
Calcula El Area Y El Perimetro De Un Triangulo Rectangulo Printable Templates Free La fórmula matemática para encontrar el perímetro del triángulo rectángulo se representa como: perímetro = a b c a b c. donde: a y b son los catetos que forman el ángulo recto. c es la hipotenusa. al desconocer uno de los lados del triángulo rectángulo es posible emplear el teorema de pitágoras. c2 = a2 b2. Ejemplo del área de un triángulo rectángulo. ahora que ya sabemos cuál es la fórmula del área de un triángulo rectángulo, vamos a resolver un ejemplo paso a paso de este tipo de triángulo. así podrás ver cómo sacar el área de un triángulo rectángulo. calcula el área del siguiente triángulo rectángulo cuyos catetos miden 3 y 4 cm. El área puede ser definida como la cantidad de espacio tomada por el objeto bidimensional. el área de un triángulo rectángulo puede ser calculada por la siguiente fórmula: a= \frac {b \times h} {2} a = 2b×h. en donde, b es la longitud de la base del triángulo y h es la longitud de la altura. derivación de la fórmula del área. Triangulo rectángulo tiene dos catetos perpendiculares y la hipotenusa – el lado más largo. la suma de los ángulos de un triángulo es de 180 °, se aplica lo siguiente: α β = 90 °. la longitud de los lados se puede determinar usando el teorema de pitágoras, los ángulos usando funciones trigonométricas.