Aplicar Propiedades De Determinantes De Matrices 45 113 Propiedades De Los Determinantes

Aplicar Propiedades De Determinantes De Matrices 45 113 Propiedades De Los Determinantes Ejercicio lleno de propiedades de determinantes. gracias por ser par. Propiedad 1: determinante de la matriz transpuesta. 2. propiedad 2: determinante con una fila o columna llena de ceros. 3. propiedad 3: determinante con dos filas o columnas iguales. 4. propiedad 4: cambiar filas o columnas de un determinante. 5. propiedad 5: multiplicar una línea de una determinante por un escalar.

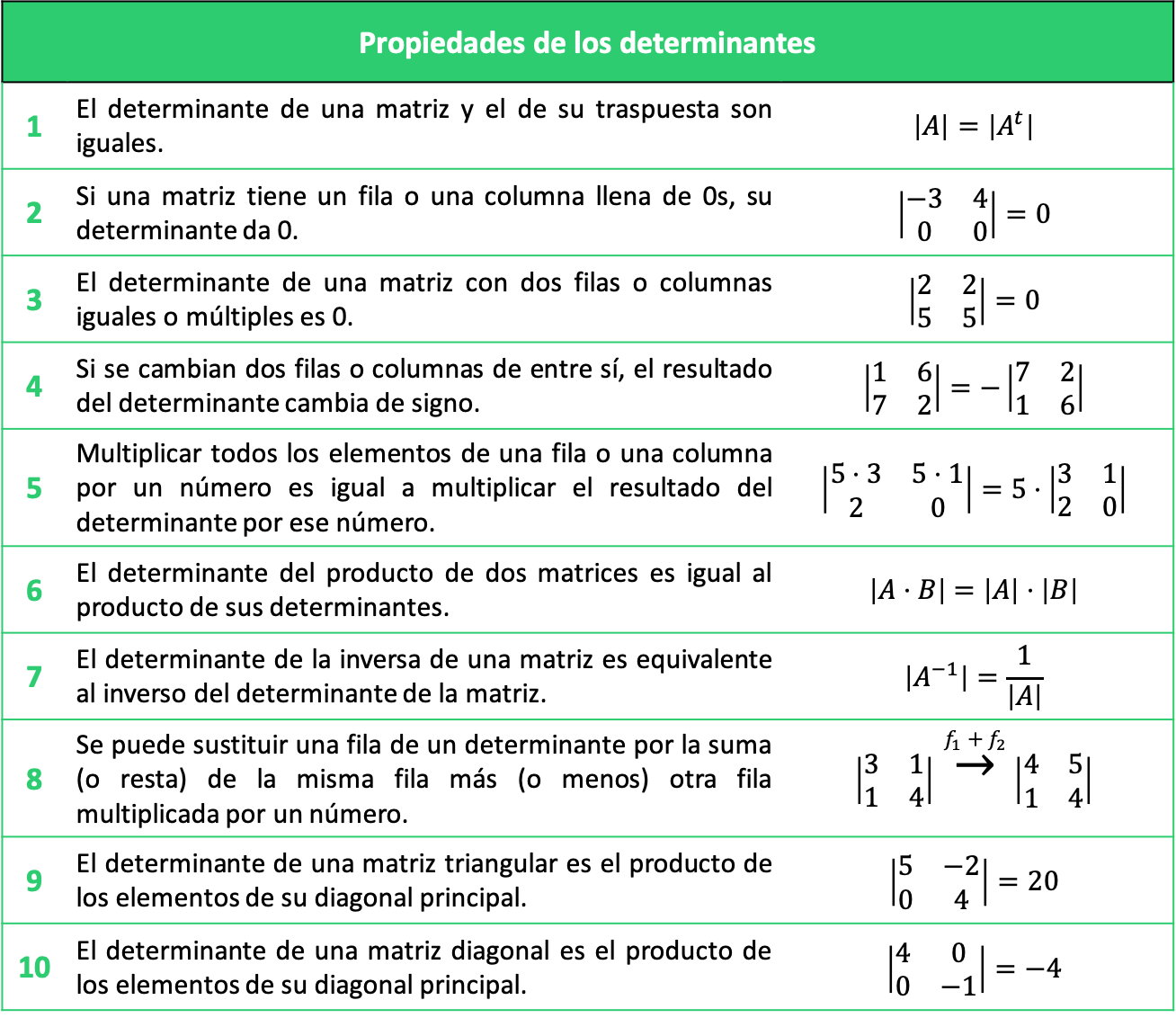
Todas Las Propiedades De Los Determinantes Con Ejercicios Ejercicios resueltos paso a paso. en esta lección vamos a ver las propiedades de los determinantes. las propiedades de los determinantes nos permiten calcular un determinante sin necesidad de desarrollarlo, lo cual es especialmente útil en determinantes cuyos elementos sean letras o que su desarrollo sea algo complejo. %pdf 1.5 %µµµµ 1 0 obj >>> endobj 2 0 obj > endobj 3 0 obj > extgstate > xobject > procset[ pdf text imageb imagec imagei] >> mediabox[ 0 0 595.32 841.92. Usando la definición 3.1.1 podemos encontrar el determinante de la siguiente manera: det (a) = 3 × 4 − 2 × 6 = 12 − 12 = 0 por teorema no3.2.7a es invertible. ahora considere la matriz b. nuevamente por definición 3.1.1 tenemos det (b) = 2 × 1 − 5 × 3 = 2 − 15 = − 13 por teorema 3.2.7b es invertible y el determinante de la. Cuadro resumen de todas las propiedades. ejercicios resueltos de propiedades de determinantes. como consecuencia , toda propiedad que sea válida para filas lo será también para columnas y viceversa. entonces llamaremos en general líneas a las filas o a las columnas. si se intercambian dos líneas de un determinate entonces cambia su signo.

Propiedades De Determinantes Usando la definición 3.1.1 podemos encontrar el determinante de la siguiente manera: det (a) = 3 × 4 − 2 × 6 = 12 − 12 = 0 por teorema no3.2.7a es invertible. ahora considere la matriz b. nuevamente por definición 3.1.1 tenemos det (b) = 2 × 1 − 5 × 3 = 2 − 15 = − 13 por teorema 3.2.7b es invertible y el determinante de la. Cuadro resumen de todas las propiedades. ejercicios resueltos de propiedades de determinantes. como consecuencia , toda propiedad que sea válida para filas lo será también para columnas y viceversa. entonces llamaremos en general líneas a las filas o a las columnas. si se intercambian dos líneas de un determinate entonces cambia su signo. Los determinantes tienen varias propiedades importantes que los hacen útiles en álgebra lineal y cálculo. a continuación se describen algunas de las propiedades más comunes: propiedad 1: el determinante de una matriz se mantiene igual si se intercambian filas o columnas. propiedad 2: el determinante de una matriz se multiplica por un. Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):.

Propiedades De Determinantes Los determinantes tienen varias propiedades importantes que los hacen útiles en álgebra lineal y cálculo. a continuación se describen algunas de las propiedades más comunes: propiedad 1: el determinante de una matriz se mantiene igual si se intercambian filas o columnas. propiedad 2: el determinante de una matriz se multiplica por un. Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):.

Propiedades De Los Determinantes Youtube