Algebra Lineal Propiedades De Los Determinantes Matrices

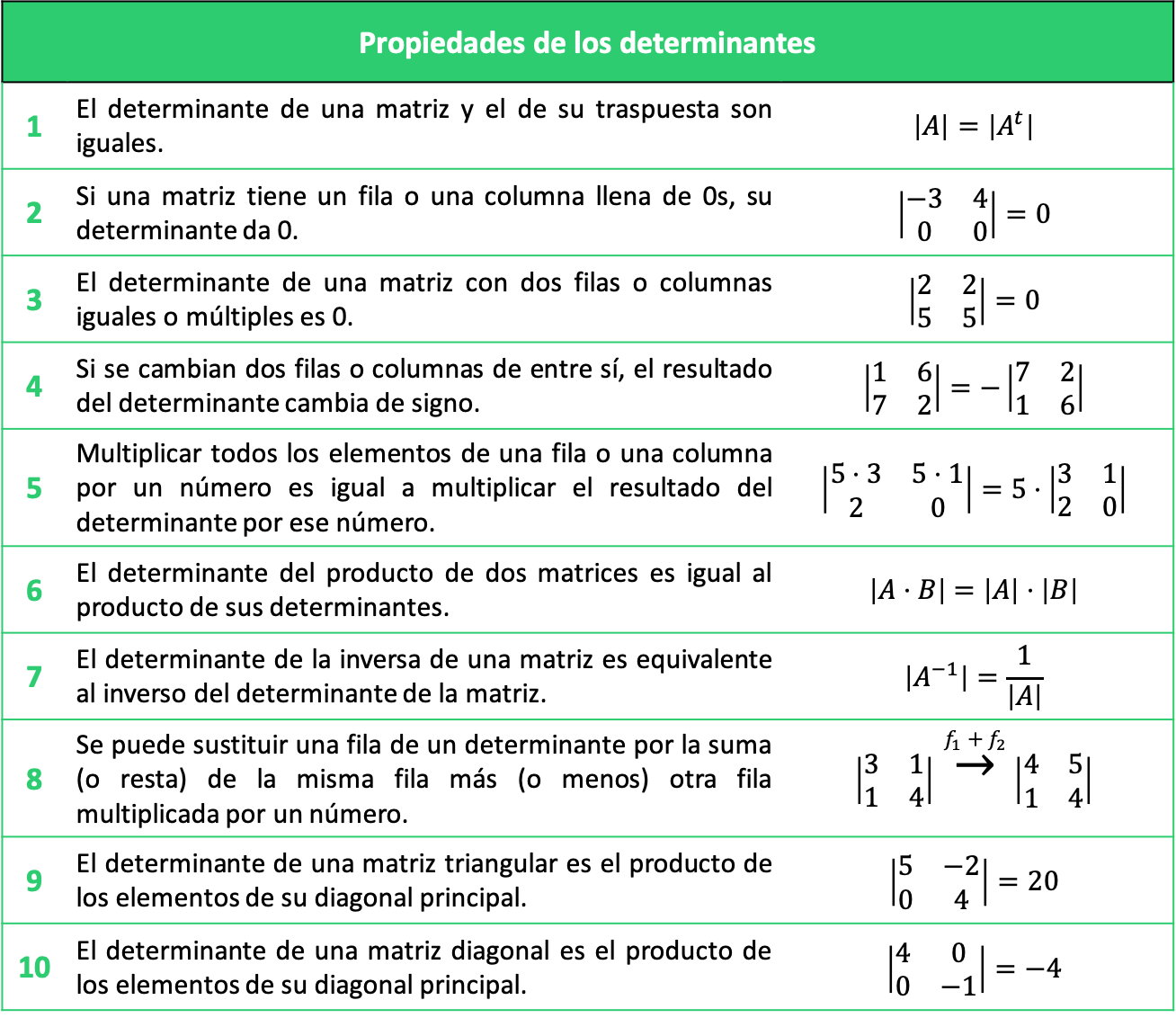
Todas Las Propiedades De Los Determinantes Con Ejercicios Propiedad 1: determinante de la matriz transpuesta. 2. propiedad 2: determinante con una fila o columna llena de ceros. 3. propiedad 3: determinante con dos filas o columnas iguales. 4. propiedad 4: cambiar filas o columnas de un determinante. 5. propiedad 5: multiplicar una línea de una determinante por un escalar. Propiedades básicas de los determinantes. las propiedades de los determinantes son cruciales para realizar cálculos eficientes y comprender el comportamiento de las matrices. a continuación, se enumeran algunas de las más importantes: determinante de la matriz identidad: el determinante de la matriz identidad es 1, es decir, det (i) = 1.

Algebra Lineal Propiedades De Los Determinantes Matrices Youtube Los determinantes tienen varias propiedades importantes que los hacen útiles en álgebra lineal y cálculo. a continuación se describen algunas de las propiedades más comunes: propiedad 1: el determinante de una matriz se mantiene igual si se intercambian filas o columnas. propiedad 2: el determinante de una matriz se multiplica por un. Propiedad 6. si se cambia el orden de n n filas o columnas, el determinante cambia de signo si n n es impar. ejemplo. esta propiedad es una consecuencia de la propiedad anterior. cambiamos la primera fila por la segunda y, después, la segunda por la tercera. el determinante debe coincidir (número par de cambios):. Usando la definición 3.1.1 podemos encontrar el determinante de la siguiente manera: det (a) = 3 × 4 − 2 × 6 = 12 − 12 = 0 por teorema no3.2.7a es invertible. ahora considere la matriz b. nuevamente por definición 3.1.1 tenemos det (b) = 2 × 1 − 5 × 3 = 2 − 15 = − 13 por teorema 3.2.7b es invertible y el determinante de la. La principal diferencia entre las matrices y los determinantes es que una matriz es una manera de expresar datos o números, en cambio, el determinante de una matriz siempre será el resultado de una operación, es decir, un único número. otra manera de diferenciar las matrices y los determinantes es mediante sus respectivas propiedades.