5 Propiedades De La Suma De Matrices Con Ejemplos Faciles

5 Propiedades De La Suma De Matrices Con Ejemplos Fáciles Propiedad cerradura. para sumar matrices se debe tener en cuenta que tengan las mismas dimensiones, es decir si quiero sumar dos matrices, ambas deben tener dimensiones m x n. veamos un ejemplo. por ejemplo, si quiero sumar una matriz 3 x 2, entonces deberá ser con otra matriz que también tenga dimensiones 3 x 2. La operación se define de una manera muy sencilla: la matriz suma de dos matrices con la misma dimensión es la matriz que tiene en la posición fila i y columna j la suma de los elementos de la misma posición en las matrices que sumamos. es decir, la suma de matrices se calcula sumando los elementos que ocupan la misma posición.

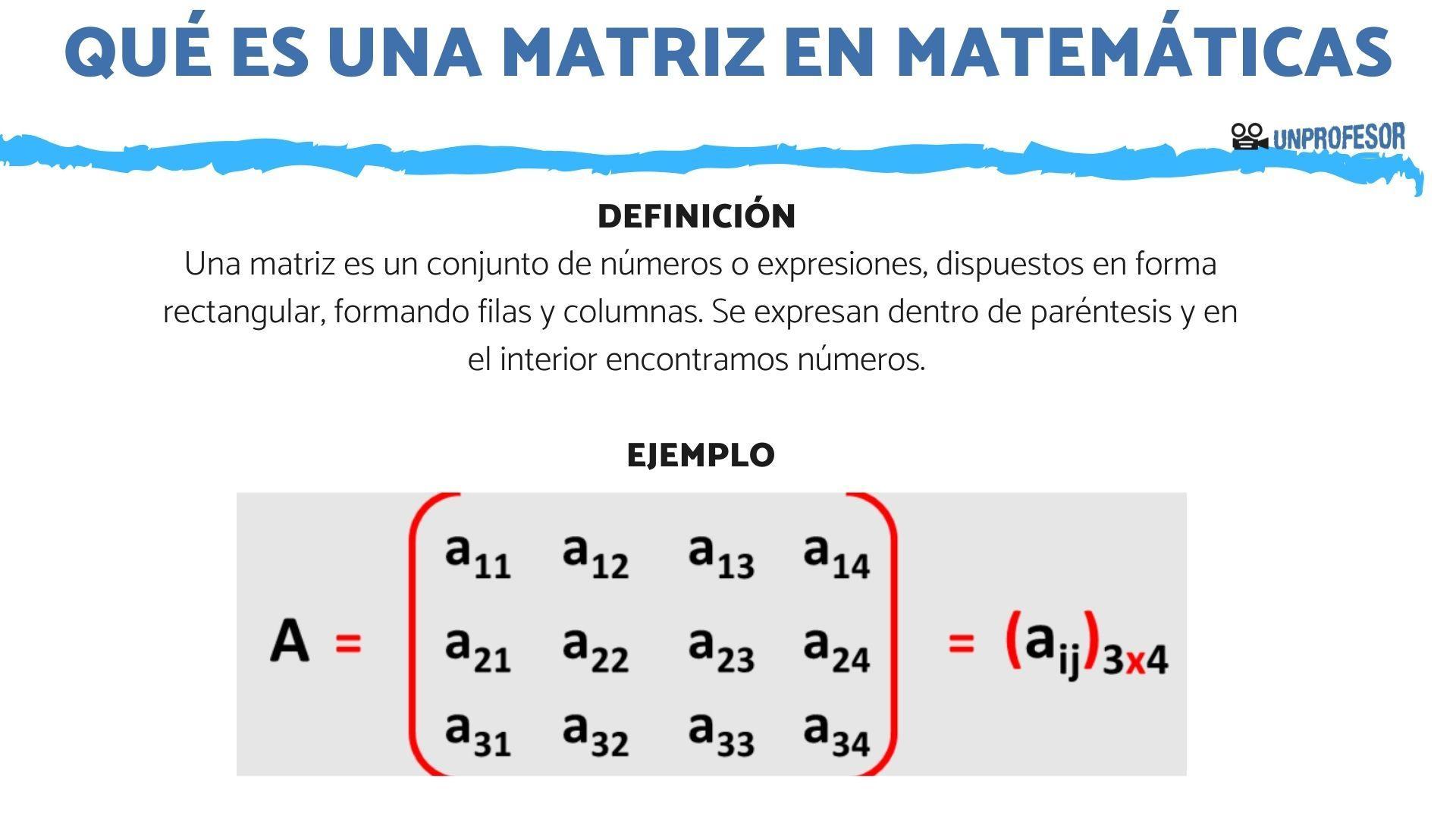
5 Propiedades De La Suma De Matrices Con Ejemplos Fáciles Para que sea posible realizar la suma de matrices, ambas matrices deben tener las mismas dimensiones. esto significa que ambas matrices deben tener el mismo número de filas y columnas. propiedades de la suma de matrices. la suma de matrices presenta varias propiedades que son fundamentales para su manejo. estas incluyen:. Conclusión: dominando la suma de matrices con facilidad. la suma de matrices es un aspecto esencial del álgebra lineal que se puede dominar con la práctica correcta. a través de ejemplos, propiedades y métodos, puedes mejorar tus habilidades y aplicar este conocimiento en diversas áreas. La suma de dos matrices se define únicamente cuando las matrices son del mismo tamaño. o sea que no es posible sumar matrices que en tamaño no sean iguales porque serían incompatibles. asumiendo este punto, entonces podemos ver la fórmula general para sumar matrices, y así poder resolver ejemplos de suma de matrices. Ejercicio 5. resuelve la siguiente suma y resta matricial: ver solución. se trata de una operación combinada de una resta y una suma de matrices cuadradas de orden 3: ahora que ya sabes cómo sumar y restar matrices, es un buen momento para ver cómo multiplicar matrices, seguramente la más importante de las operaciones con matrices.

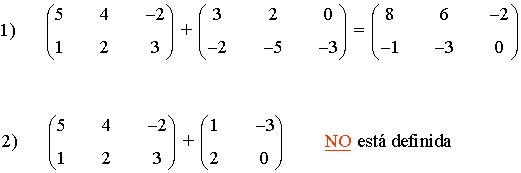
Suma De Matrices Propiedades De La Suma De Matrices Diferencia De Matrices Ejemplos Y Gráficos La suma de dos matrices se define únicamente cuando las matrices son del mismo tamaño. o sea que no es posible sumar matrices que en tamaño no sean iguales porque serían incompatibles. asumiendo este punto, entonces podemos ver la fórmula general para sumar matrices, y así poder resolver ejemplos de suma de matrices. Ejercicio 5. resuelve la siguiente suma y resta matricial: ver solución. se trata de una operación combinada de una resta y una suma de matrices cuadradas de orden 3: ahora que ya sabes cómo sumar y restar matrices, es un buen momento para ver cómo multiplicar matrices, seguramente la más importante de las operaciones con matrices. Ejemplos y gráficos. suma de matrices. la suma de dos matrices a = ( a ij ) y b = ( b ij ) de la misma dimensión m × n, es otra matriz que representamos como a b, de la misma dimensión que a y b, cuyos elementos son la suma de los elementos situados en las mismas posiciones, es decir, a b = (a ij b ij). Podemos utilizar esta propiedad en la suma de matrices. siempre que sumemos la matriz cero a cualquier matriz, obtendremos como resultado esa misma matriz. veamos un ejemplo . siendo a = 5 9 3 y o = 0 0 0 . 4 1 6 0 0 0 ; con dos matrices de orden 2x3 podemos aplicar la propiedad y realizar la operación suma.

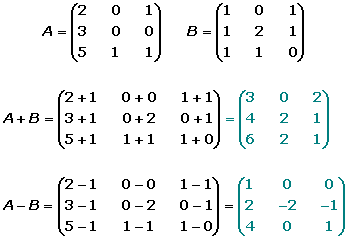
Cómo Sumar Matrices Una Guía Simple Para Principiantes Ejemplos y gráficos. suma de matrices. la suma de dos matrices a = ( a ij ) y b = ( b ij ) de la misma dimensión m × n, es otra matriz que representamos como a b, de la misma dimensión que a y b, cuyos elementos son la suma de los elementos situados en las mismas posiciones, es decir, a b = (a ij b ij). Podemos utilizar esta propiedad en la suma de matrices. siempre que sumemos la matriz cero a cualquier matriz, obtendremos como resultado esa misma matriz. veamos un ejemplo . siendo a = 5 9 3 y o = 0 0 0 . 4 1 6 0 0 0 ; con dos matrices de orden 2x3 podemos aplicar la propiedad y realizar la operación suma.

Suma De Matrices Diccionario De Matemáticas Superprof